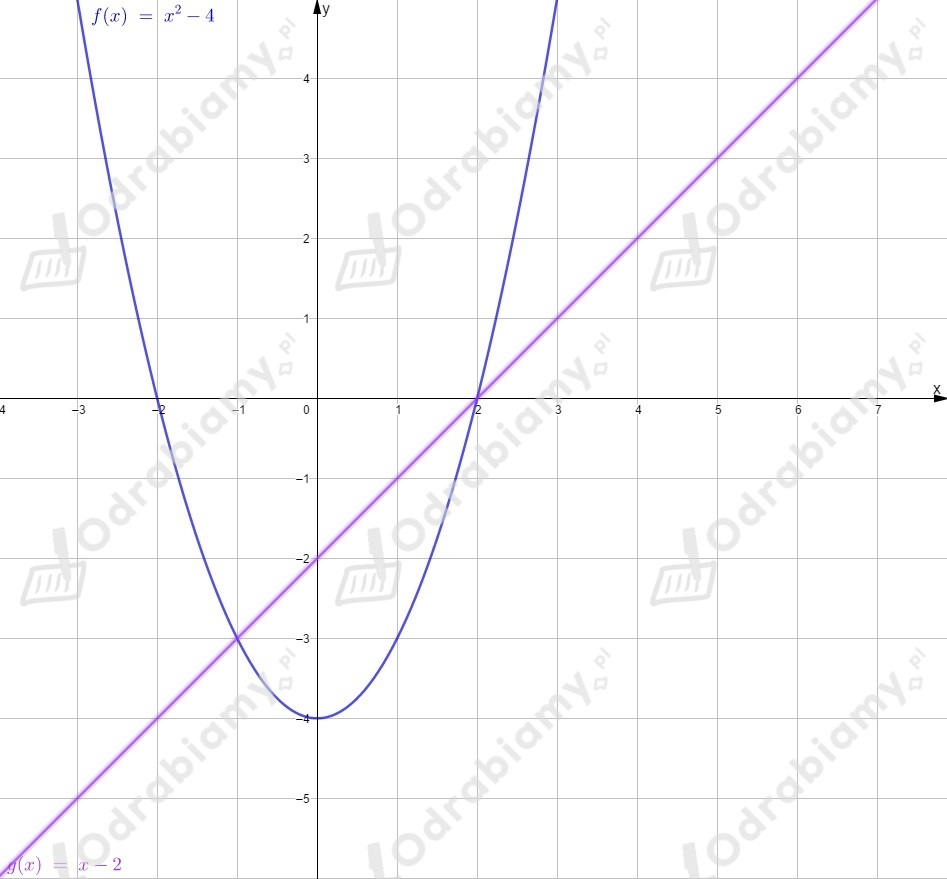
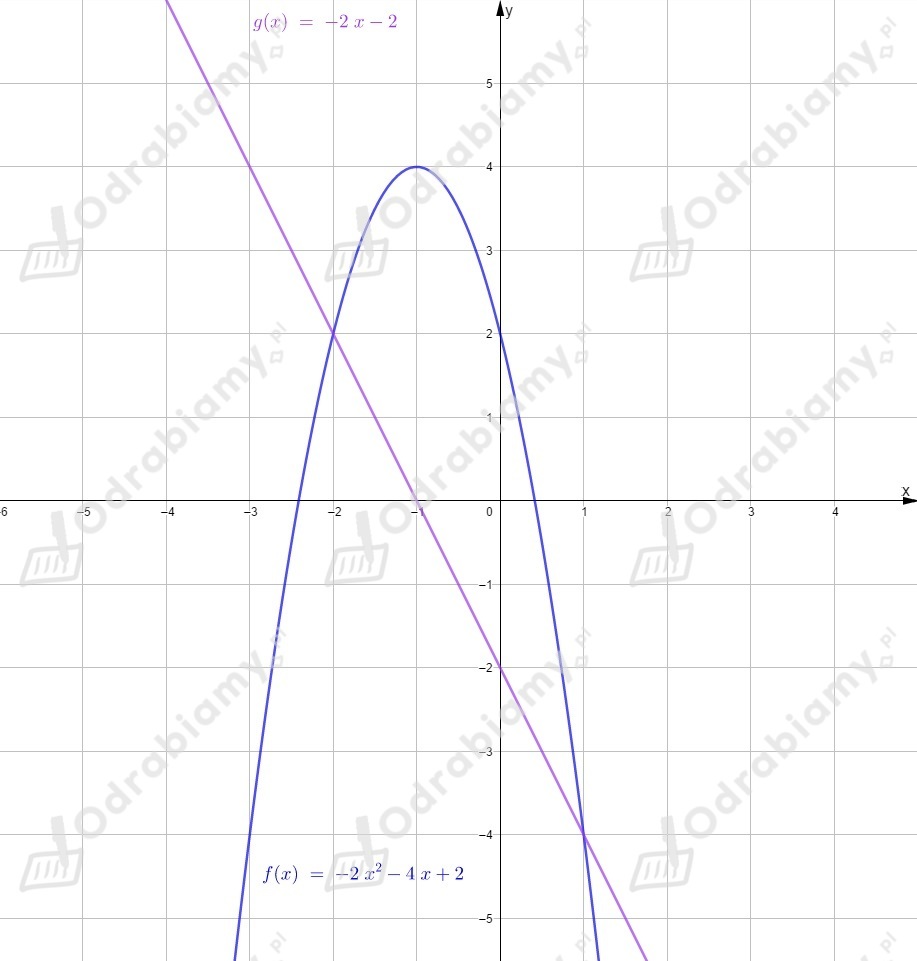
Obliczamy wartości funkcji w kilku punktach, aby narysować wykres.

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży nad wykresem funkcji )

 dla . 

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży pod wykresem funkcji )

 dla .

Na koniec sprawdzamy, w których punktach funkcje  i  się przecinają

 dla .

Teraz rozwiążemy nierówność  sposobem rachunkowym

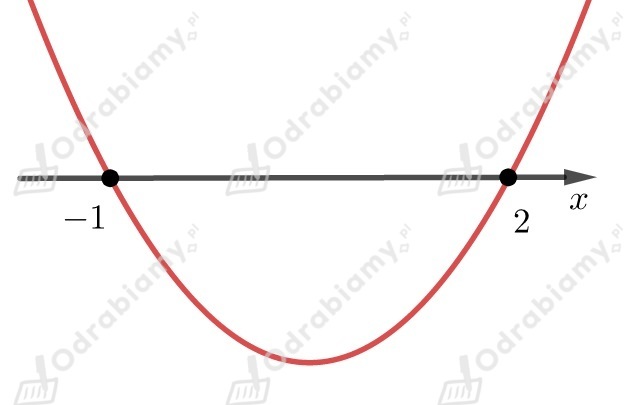
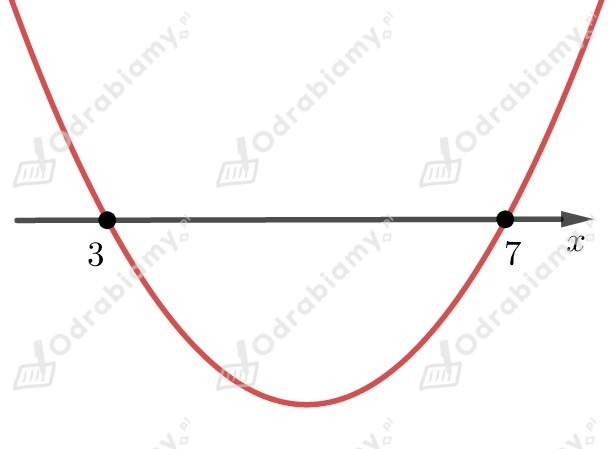
Obliczamy  i miejsca zerowe funkcji

Współczynnik przy najwyższej potędze jest liczbą większą od zera 

,

dlatego ramiona paraboli skierowane są do góry.

Odczytujemy z wykresu dla jakich  nierówność  jest spełniona

.

Przedział jest obustronnie otwarty, ponieważ szukamy takich ,

dla których  jest większe od  i nie równe .

 Obliczamy wartości funkcji w kilku punktach, aby narysować wykres.

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży nad wykresem funkcji )

 dla . 

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży pod wykresem funkcji )

 dla .

Na koniec sprawdzamy, w których punktach funkcje  i  się przecinają

 dla .

Teraz rozwiążemy nierówność  sposobem rachunkowym

Każda liczba podniesiona do potęgi  jest większa lub równa  ( ),

więc nierówność  nie jest prawdziwa, dlatego zbiorem jej rozwiązań jest zbiór pusty

 .

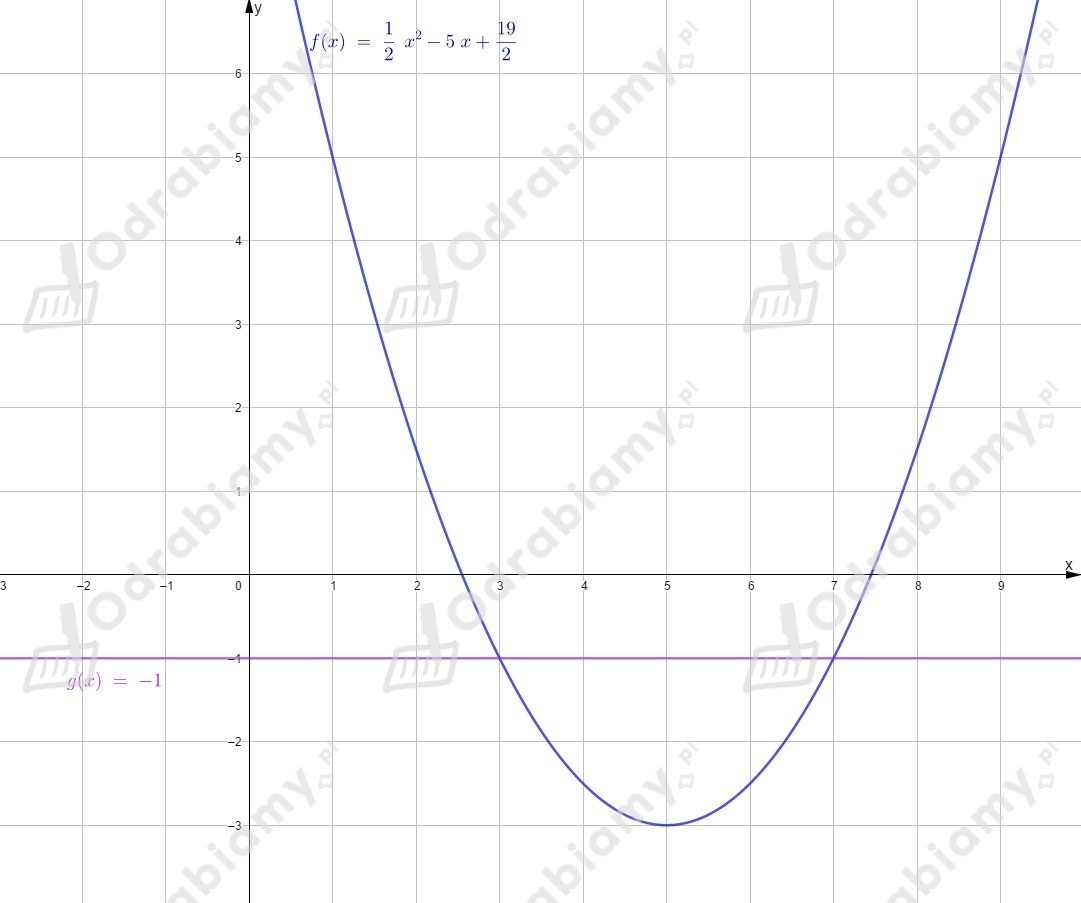
 Obliczamy wartości funkcji w kilku punktach, aby narysować wykres.

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży nad wykresem funkcji )

 dla . 

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży pod wykresem funkcji )

 dla .

Na koniec sprawdzamy, w których punktach funkcje  i  się przecinają

 dla .

Teraz rozwiążemy nierówność  sposobem rachunkowym

Obliczamy  i miejsca zerowe funkcji

Współczynnik przy najwyższej potędze jest liczbą większą od zera 

,

dlatego ramiona paraboli skierowane są do góry.

Odczytujemy z wykresu dla jakich  nierówność  jest spełniona

.

Przedział jest obustronnie otwarty, ponieważ szukamy takich ,

dla których  jest większe od  i nie równe .

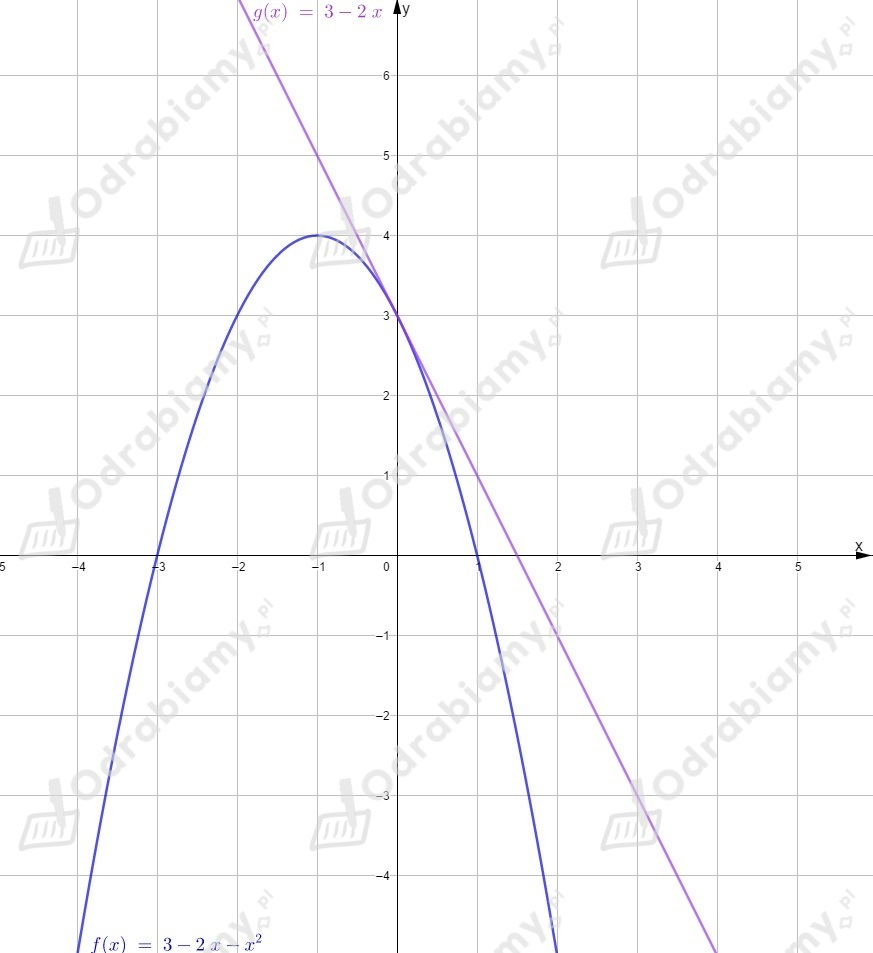
 Obliczamy wartości funkcji w kilku punktach, aby narysować wykres.

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży nad wykresem funkcji )

 dla . 

Odczytujemy z wykresu rozwiązanie nierówności  

(sprawdzamy dla jakich   wykres funkcji  leży pod wykresem funkcji )

 dla .

Na koniec sprawdzamy, w których punktach funkcje  i  się przecinają

 dla .

Teraz rozwiążemy nierówność  sposobem rachunkowym

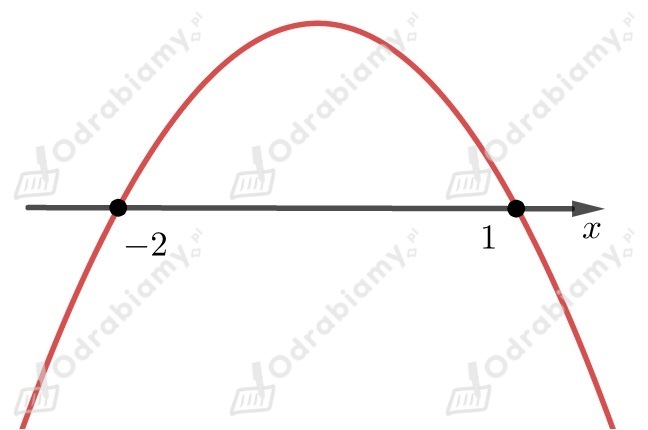
Obliczamy  i miejsca zerowe funkcji

Współczynnik przy najwyższej potędze jest liczbą mniejszą od zera 

dlatego ramiona paraboli skierowane są do dołu.

Odczytujemy z wykresu dla jakich  nierówność  jest spełniona

.

Przedział jest obustronnie otwarty, ponieważ szukamy takich ,

dla których  jest większe od  i nie równe .