Jeśli przesuniemy wykres funkcji   o wektor    to otrzymamy funkcję:

.

Wykres funkcji  otrzymujemy przez odbicie wykresu funkcji  względem osi .

Wykresy  i  są symetryczne względem osi .

Wykres funkcji  otrzymujemy przez odbicie wykresu funkcji  względem osi .

Wykresy  i  są symetryczne względem osi .

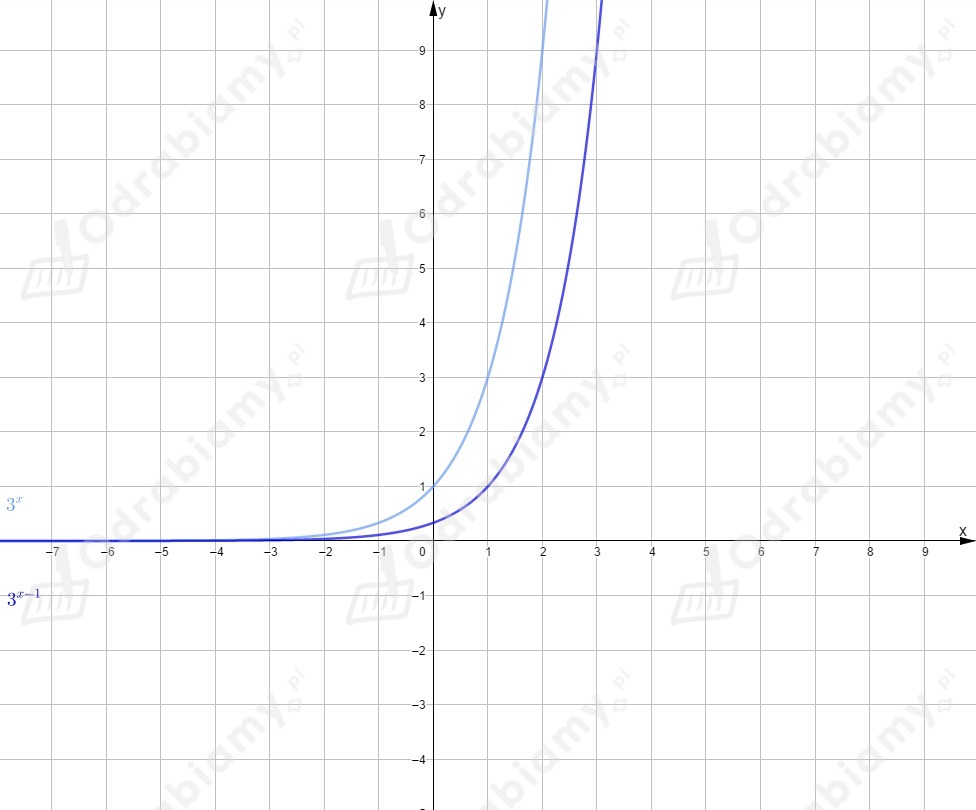
Rysujemy wykres funkcji .

Rysujemy wykres funkcji .

Odczytujemy zbiór argumentów, dla których wartość funkcji  jest mniejsza lub

równa od wartości funkcji   (dla jakich  wykres funkcji  leży pod wykresem

funkcji  lub pokrywa się z nim)

.

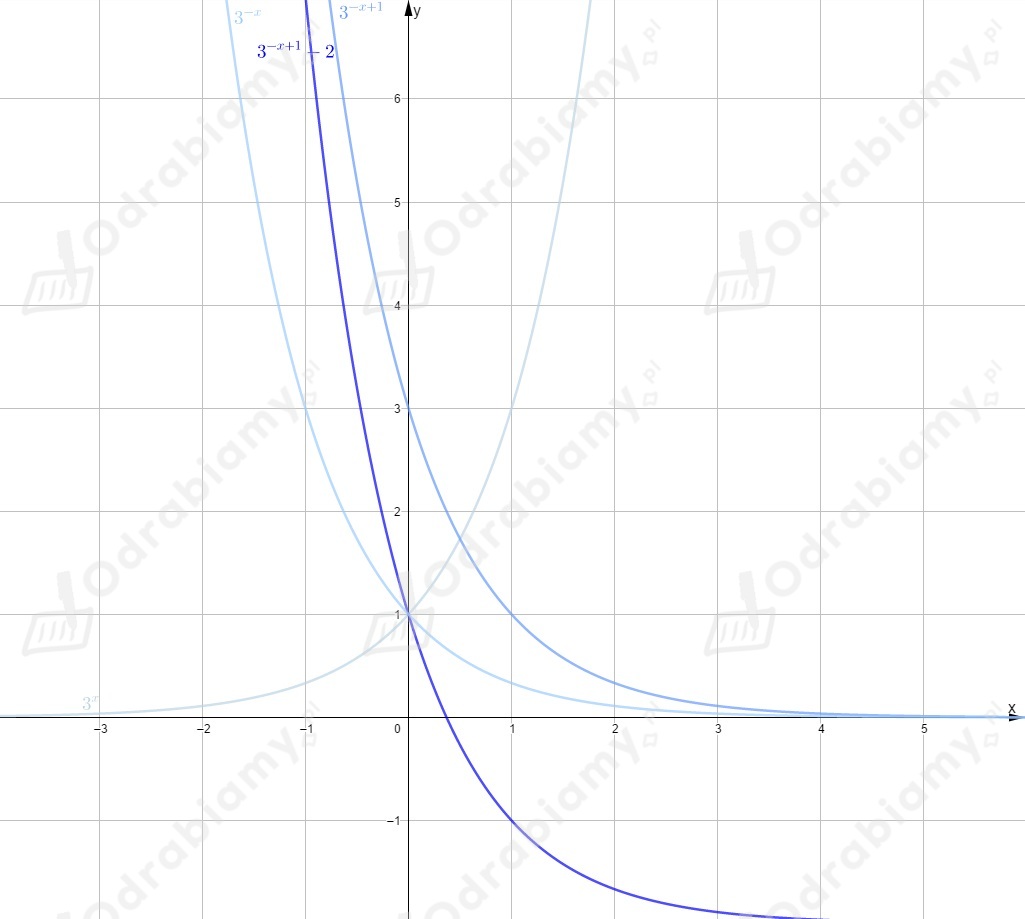
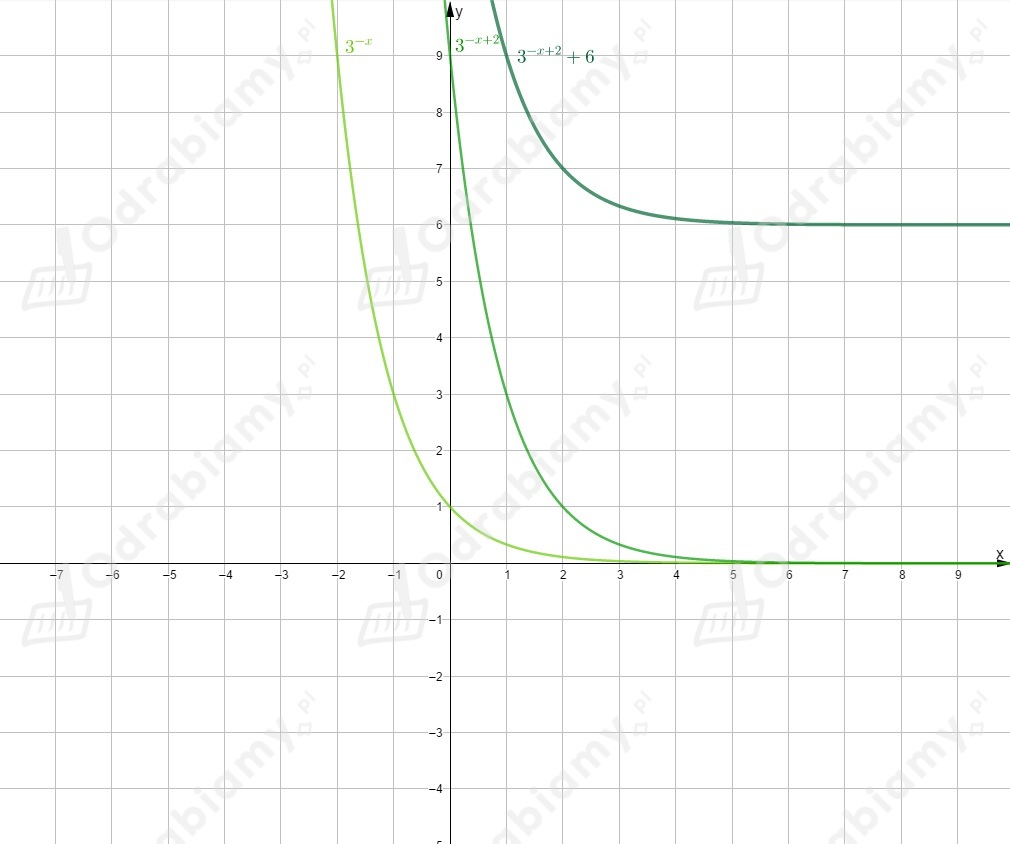
Rysujemy wykres funkcji . i odbijamy go symetrycznie względem osi y.

Otrzymujemy wykres funkcji .

Następnie przesuwamy go o  jednostkę w lewo wzdłuż osi  

i o  jednostki w dół wzdłuż osi .

Rysujemy wykres prostej  .

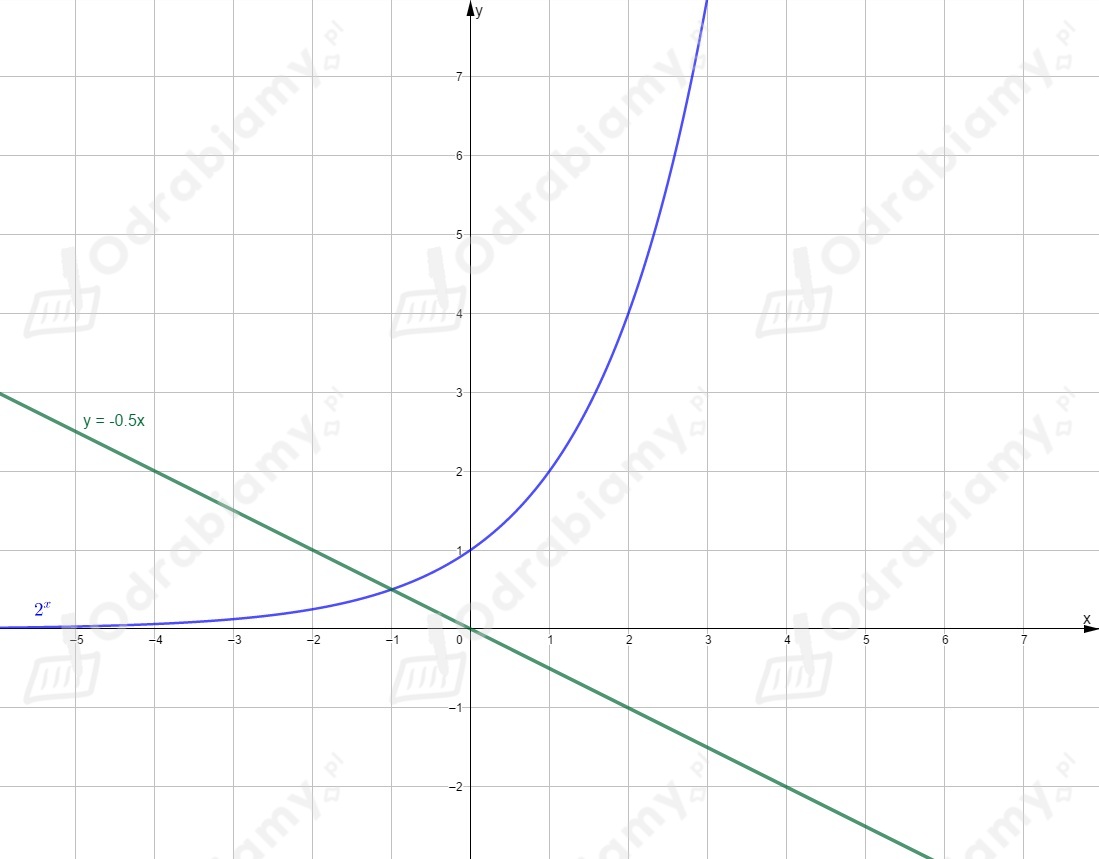
Odczytujemy zbiór argumentów, dla których wartość funkcji  jest większa od

wartości funkcji   (dla jakich  wykres funkcji  leży nad wykresem funkcji )

.

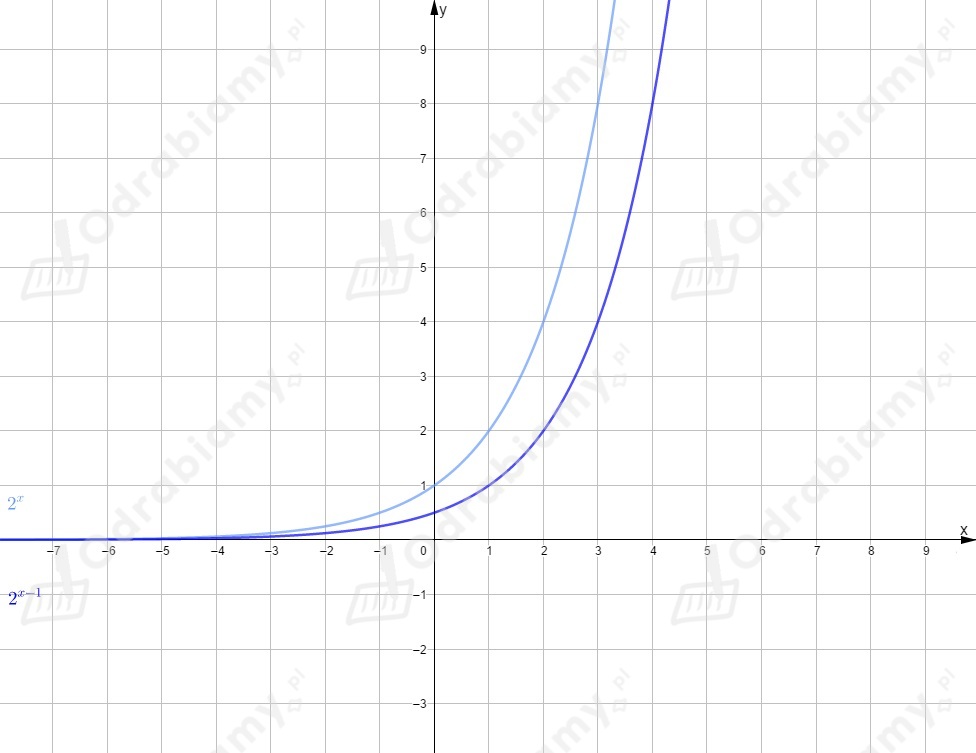
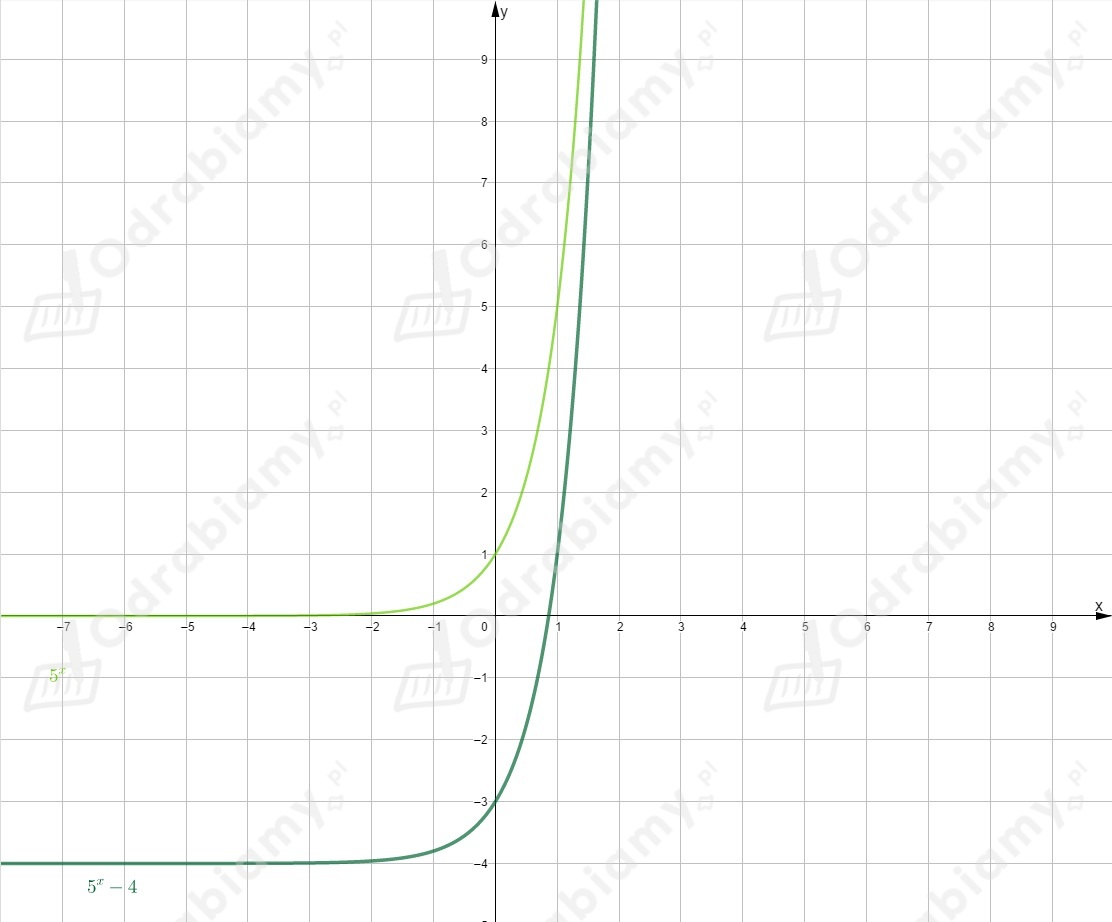
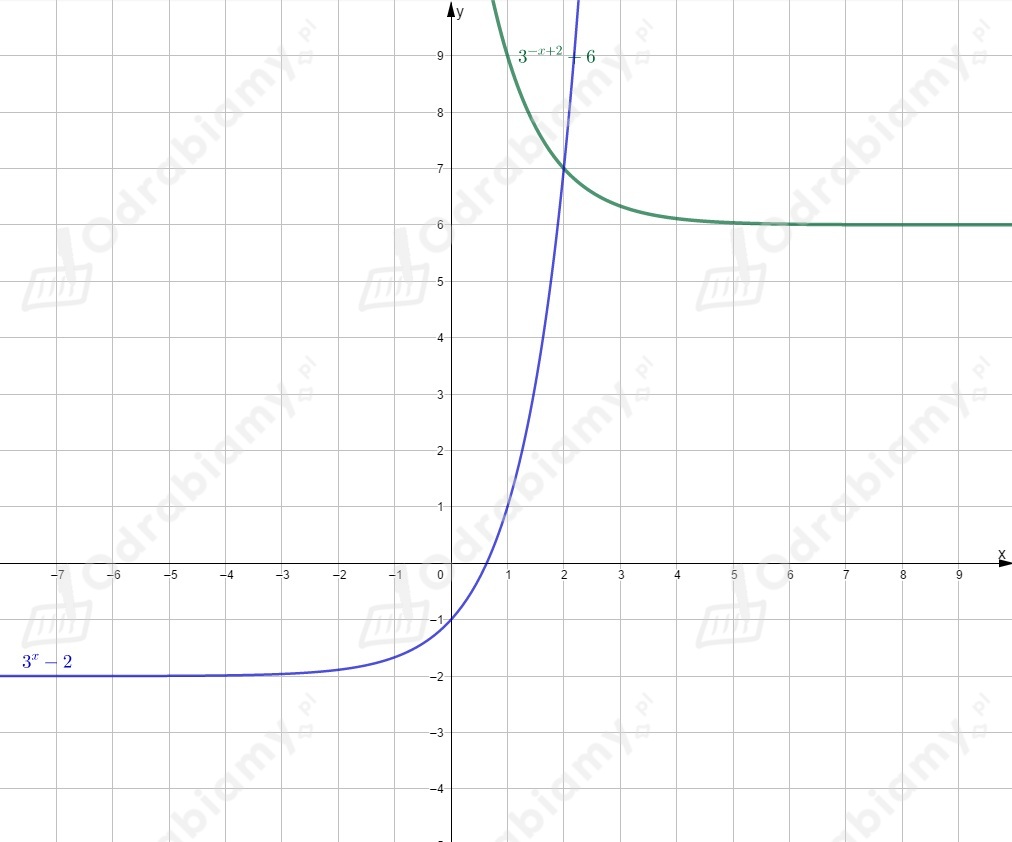
Rysujemy wykres funkcji  i przesuwamy go o  jednostkę w prawo wzdłuż osi .

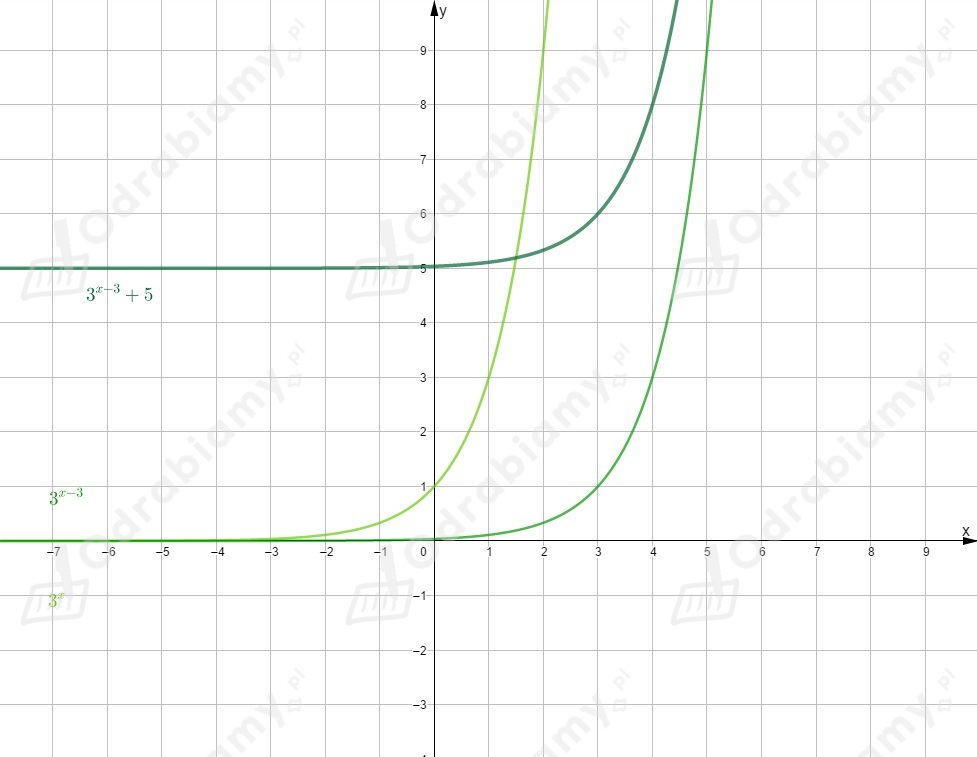
Rysujemy wykres funkcji  i przesuwamy go o  jednostki w prawo wzdłuż osi  

i o  jednostek w górę wzdłuż osi . 

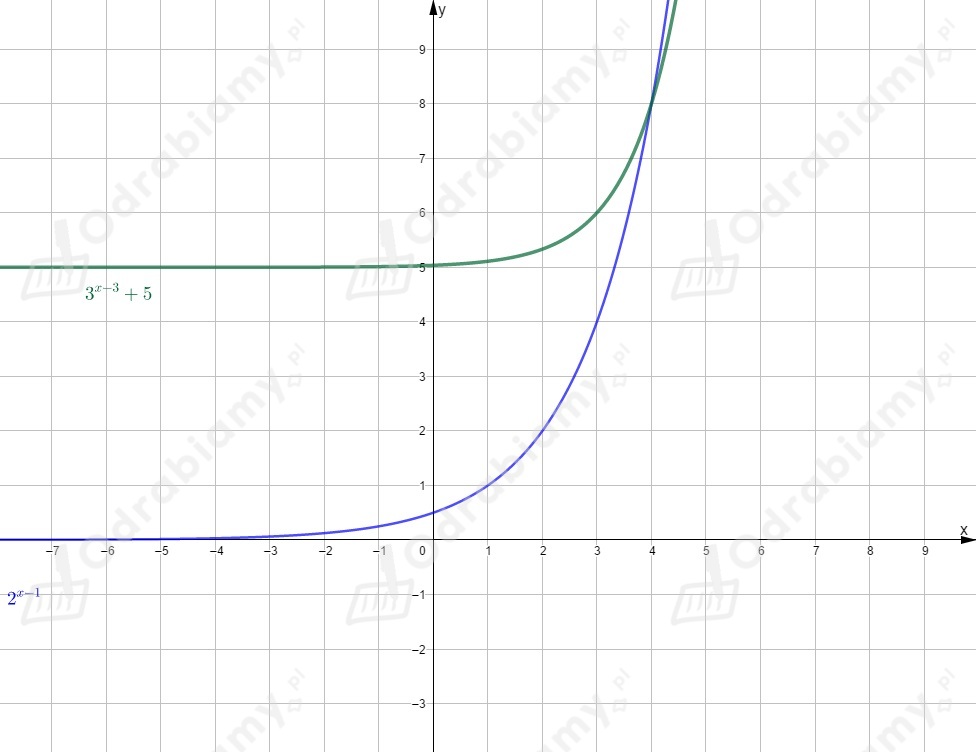
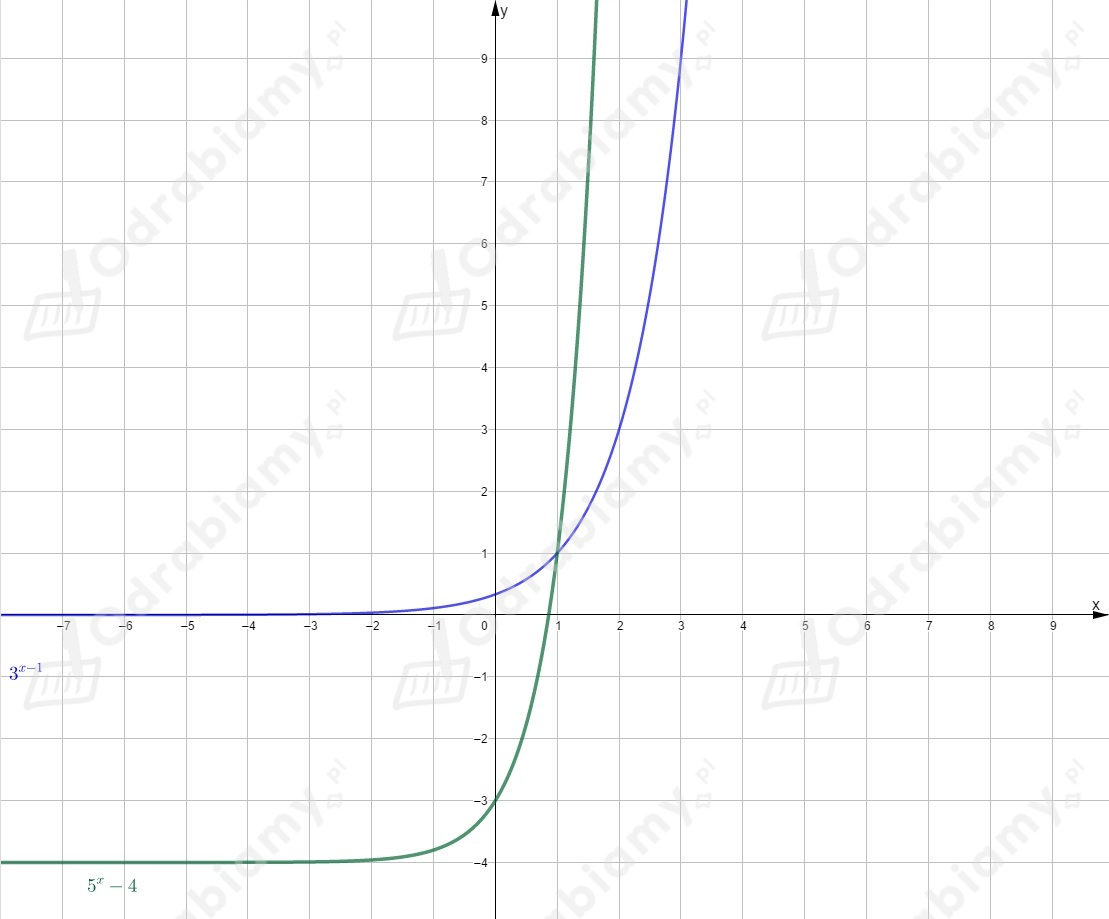
Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy zbiór argumentów, dla których wartość funkcji  jest większa od

wartości funkcji   (dla jakich  wykres funkcji  leży nad wykresem funkcji )

.

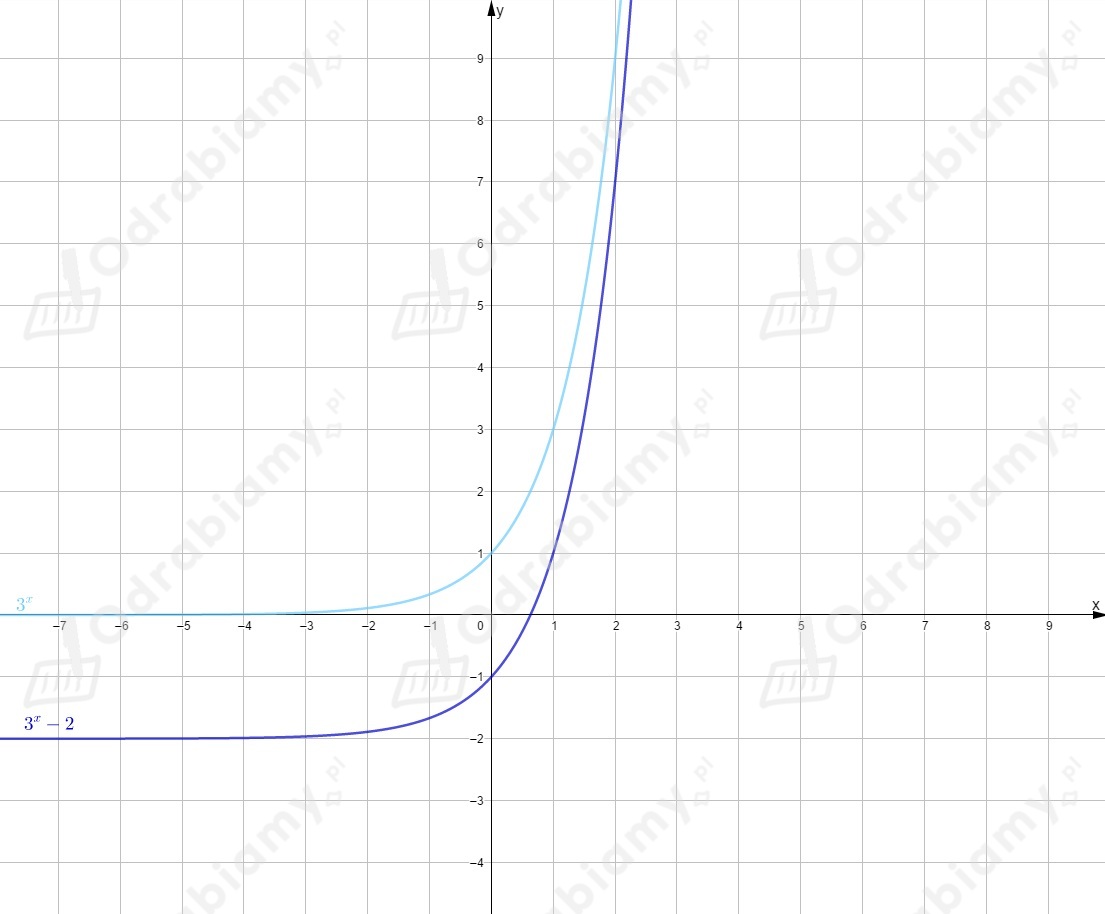
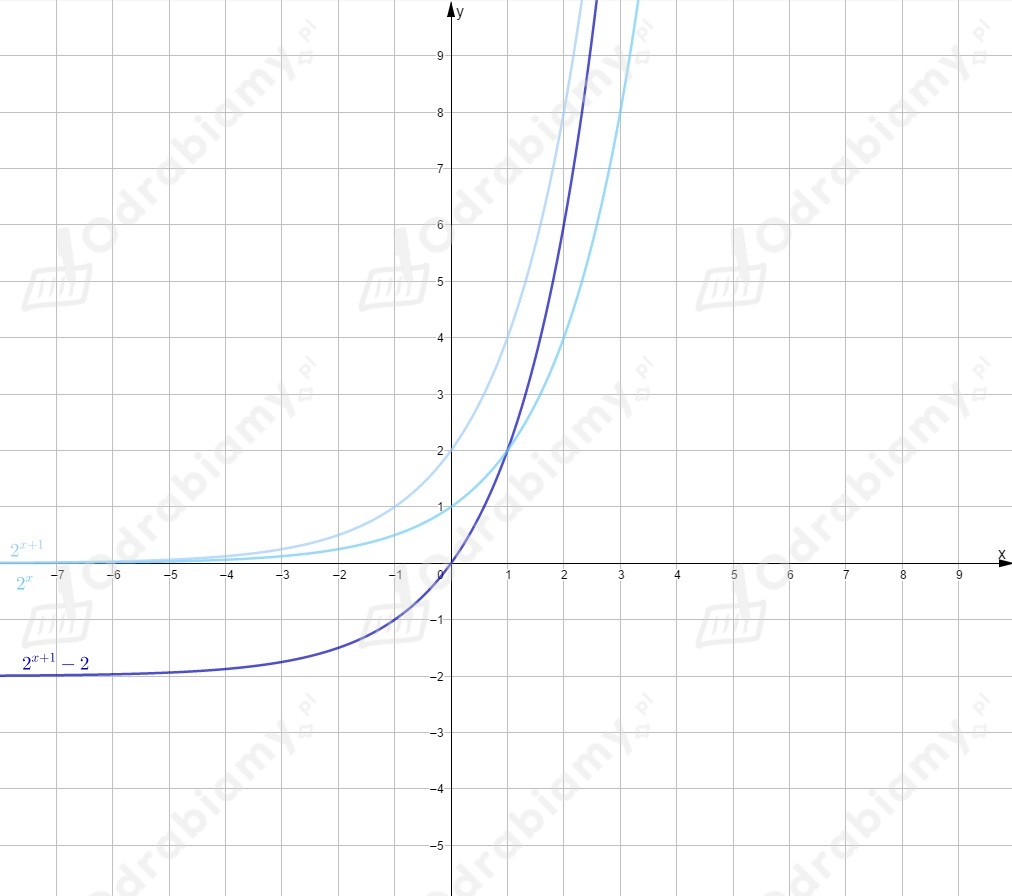
Rysujemy wykres funkcji  i przesuwamy go o  jednostkę w prawo wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o  jednostki w dół wzdłuż osi .

Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy zbiór argumentów, dla których wartość funkcji  jest większa 

od wartości funkcji   (dla jakich  wykres funkcji  leży nad wykresem

funkcji )

.

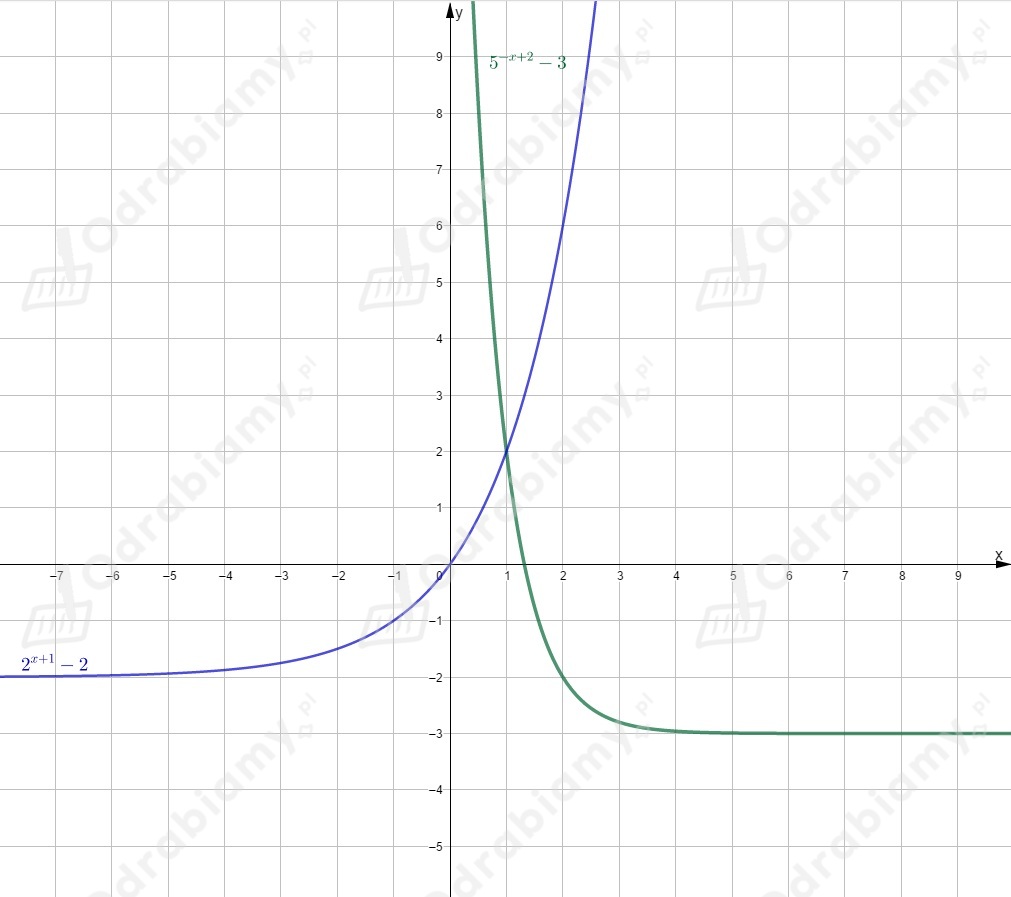
Rysujemy wykres funkcji  i przesuwamy go o  jednostki w dół wzdłuż osi .

Rysujemy wykres funkcji  i odbijamy go symetrycznie względem osi y.

Otrzymujemy wykres funkcji .

Następnie przesuwamy go o  jednostki w lewo wzdłuż osi  

i o  jednostek w górę wzdłuż osi .

Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy zbiór argumentów, dla których wartość funkcji  jest mniejsza lub

równa od wartości funkcji   (dla jakich  wykres funkcji  leży pod wykresem

funkcji  lub pokrywa się z nim).

.

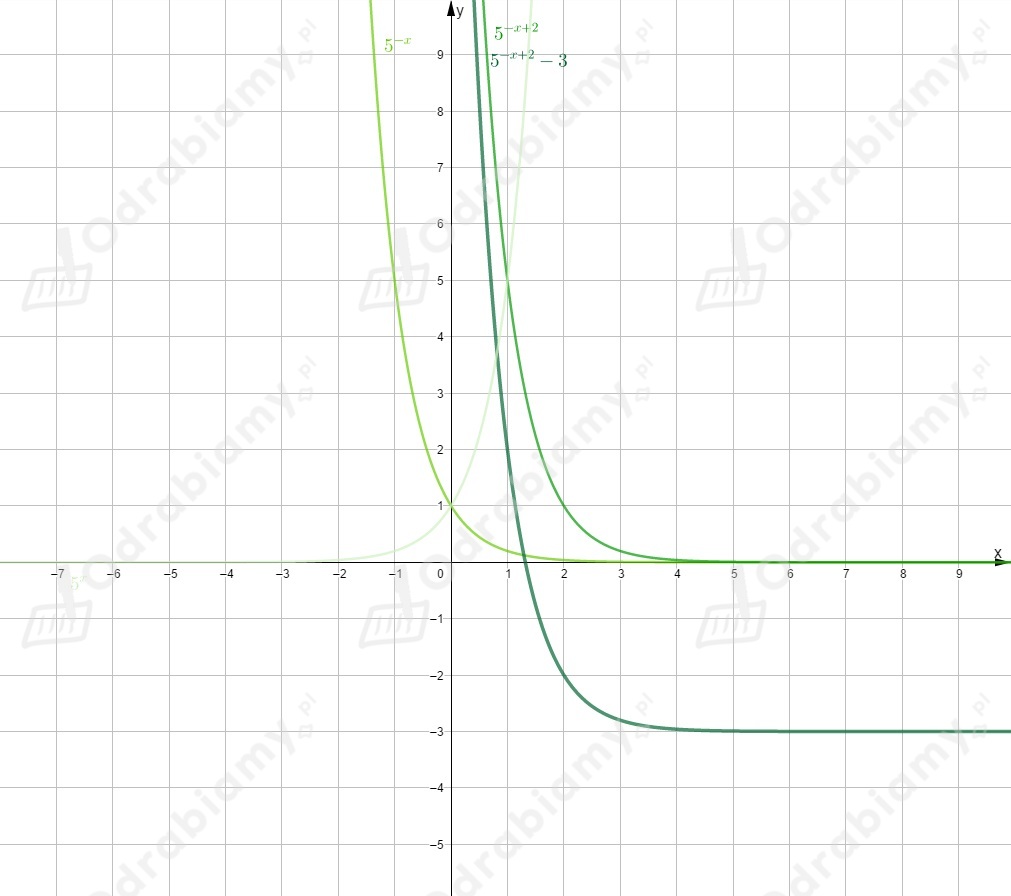
Rysujemy wykres funkcji  i odbijamy go symetrycznie względem osi y.

Otrzymujemy wykres funkcji .

Następnie przesuwamy go o  jednostki w lewo wzdłuż osi  

i o  jednostki w dół wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o  jednostki w lewo wzdłuż osi  

i o  jednostki w dół wzdłuż osi .

Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy zbiór argumentów, dla których wartość funkcji  jest większa lub

równa od wartości funkcji   (dla jakich  wykres funkcji  leży nad wykresem

funkcji  lub pokrywa się z nim).

.