Jeśli przesuniemy wykres funkcji   o wektor    to otrzymamy funkcję:

.

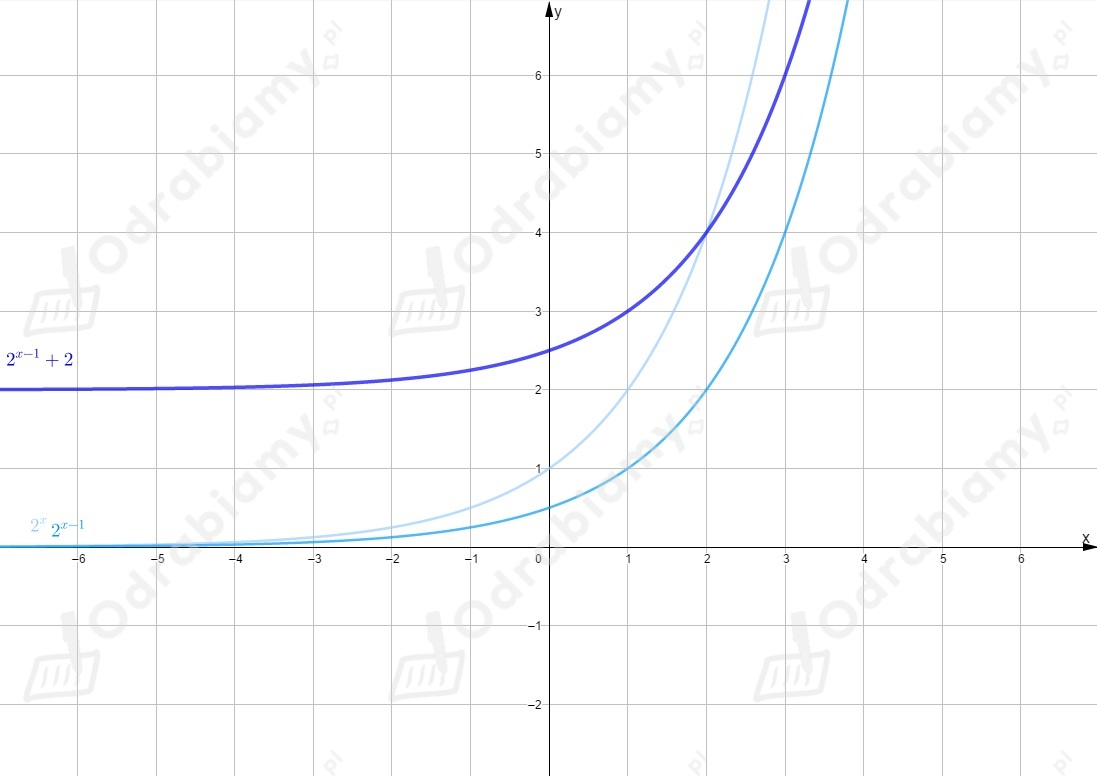
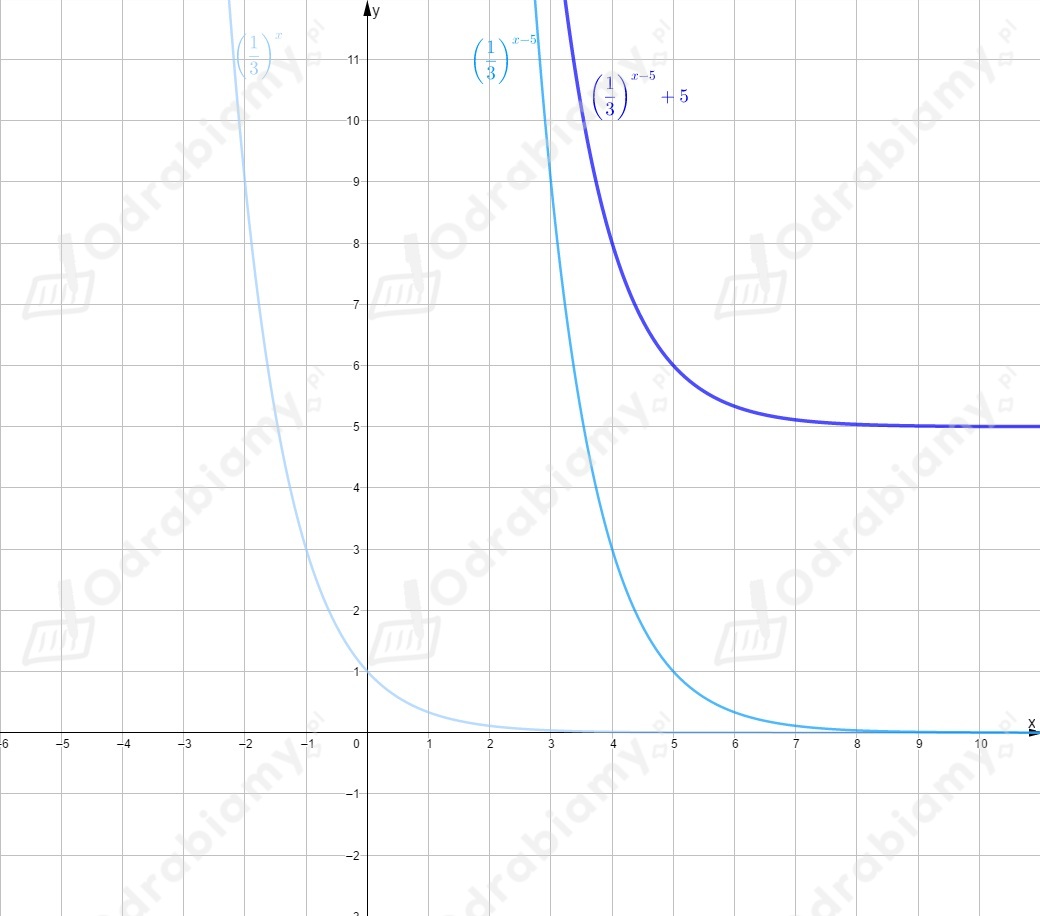
Wykres tej funkcji powstał w wyniku przesunięcia wykresu funkcji  

o  jednostkę w prawo wzdłuż osi  i o  jednostki w górę wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o wektor .

Funkcja nie przecina osi   w żadnym punkcie. 

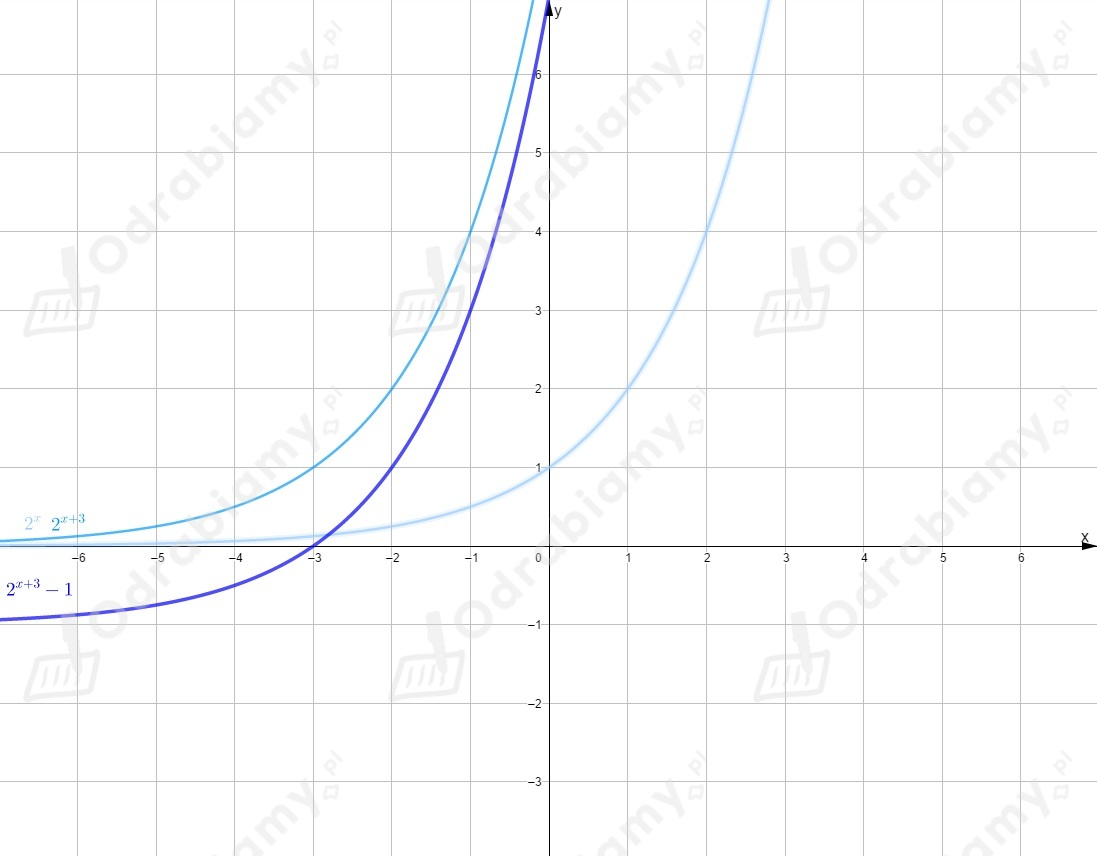
Wykres tej funkcji powstał w wyniku przesunięcia wykresu funkcji  

o  jednostki w lewo wzdłuż osi  i o  jednostkę w dół wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o wektor .

Funkcja przecina oś   w punkcie o współrzędnych .

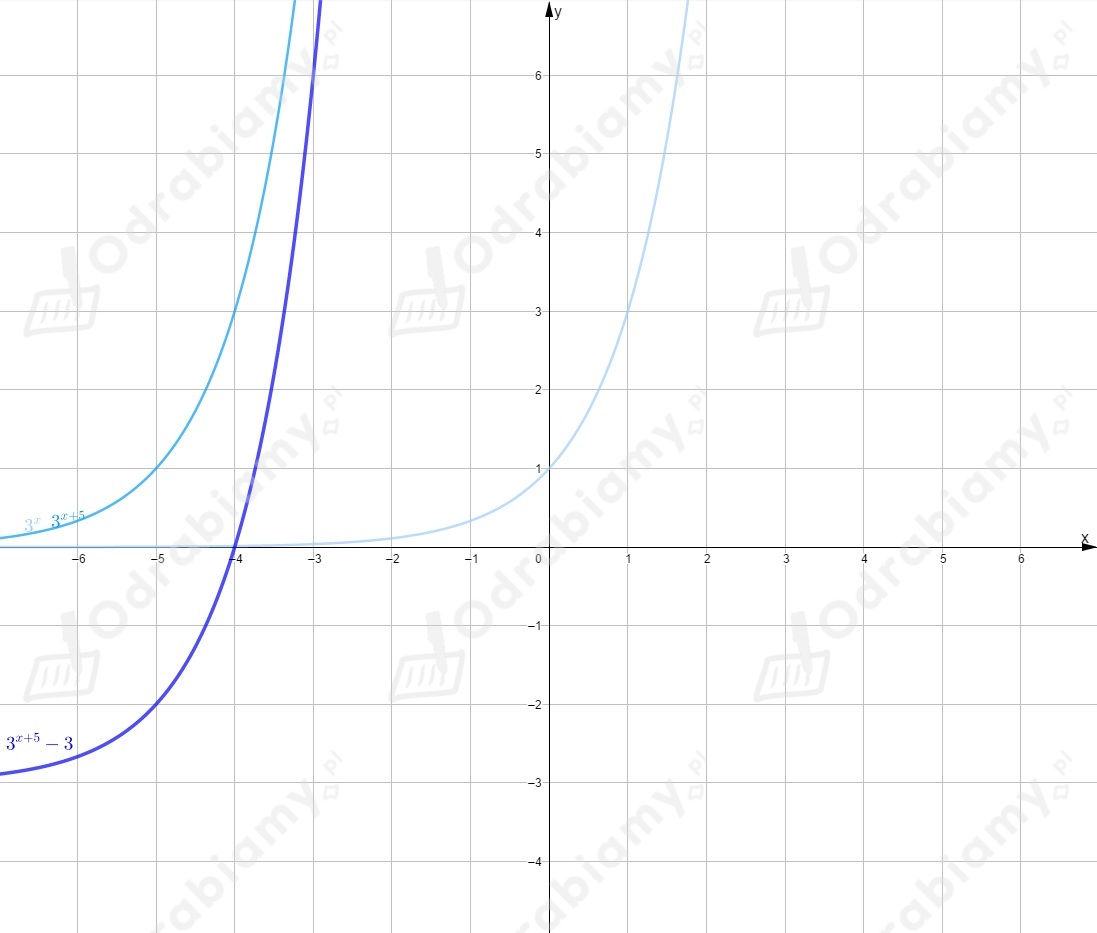
Wykres tej funkcji powstał w wyniku przesunięcia wykresu funkcji  

o  jednostek w lewo wzdłuż osi  i o  jednostki w dół wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o wektor .

Funkcja przecina oś   w punkcie o współrzędnych .

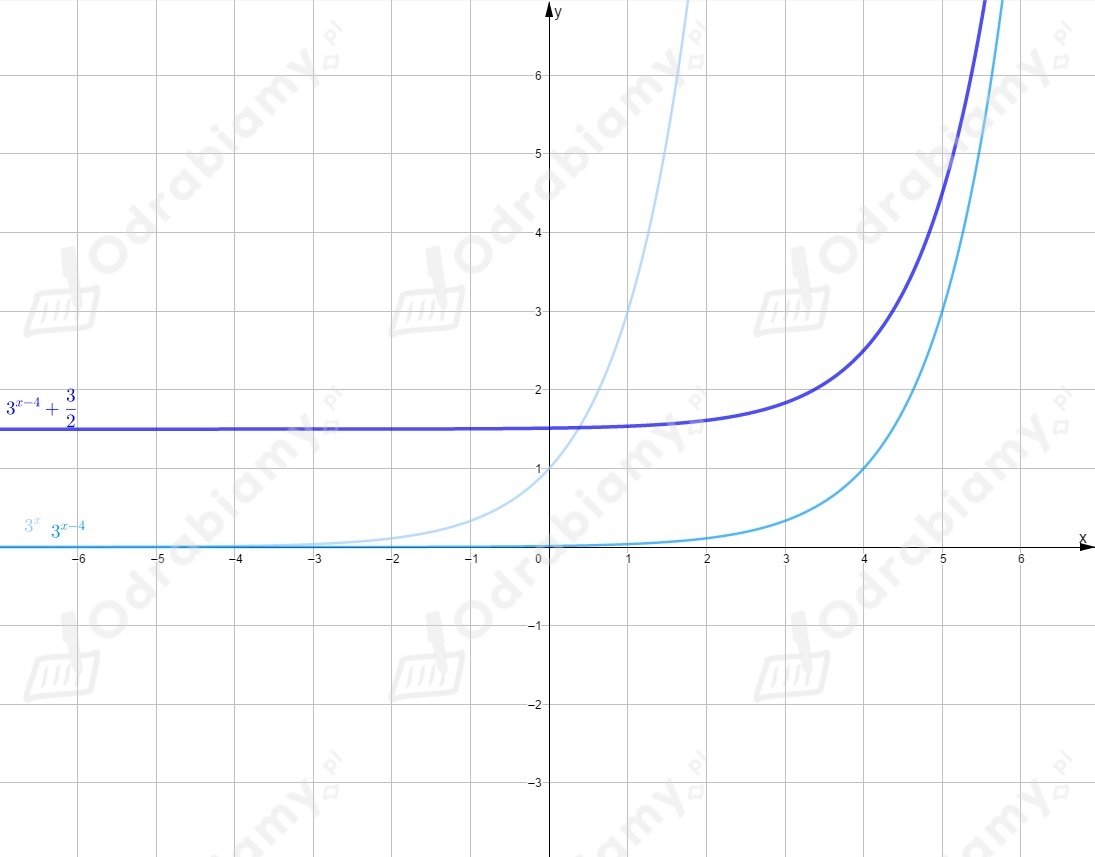
Wykres tej funkcji powstał w wyniku przesunięcia wykresu funkcji  

o  jednostki w prawo wzdłuż osi  i o  jednostki w górę wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o wektor .

Funkcja nie przecina osi   w żadnym punkcie.

Wykres tej funkcji powstał w wyniku przesunięcia wykresu funkcji  

o  jednostki w lewo wzdłuż osi  i o  jednostki w dół wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o wektor .

Funkcja przecina oś   w punkcie o współrzędnych .

Wykres tej funkcji powstał w wyniku przesunięcia wykresu funkcji  

o  jednostek w prawo wzdłuż osi  i o  jednostek w górę wzdłuż osi .

Rysujemy wykres funkcji  i przesuwamy go o wektor .

Funkcja nie przecina osi   w żadnym punkcie.