Wykres funkcji   otrzymujemy po przesunięciu wykresu funkcji   o wektor  .

Wykresy funkcji   powstały w wyniku przesunięcia wykresu funkcji  wzdłuż osi . 

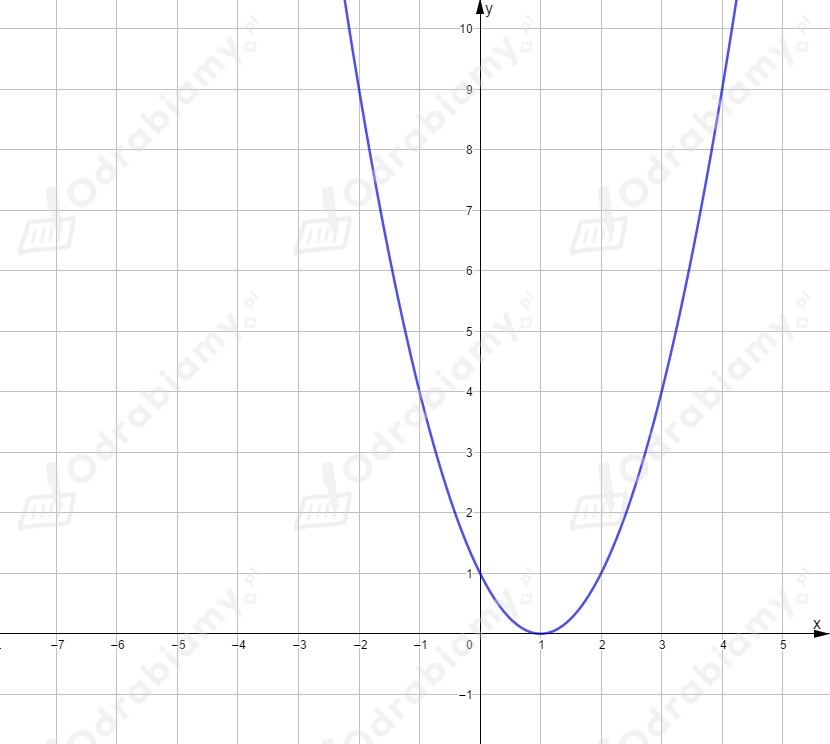
Podstawiając za     otrzymamy wykres  .

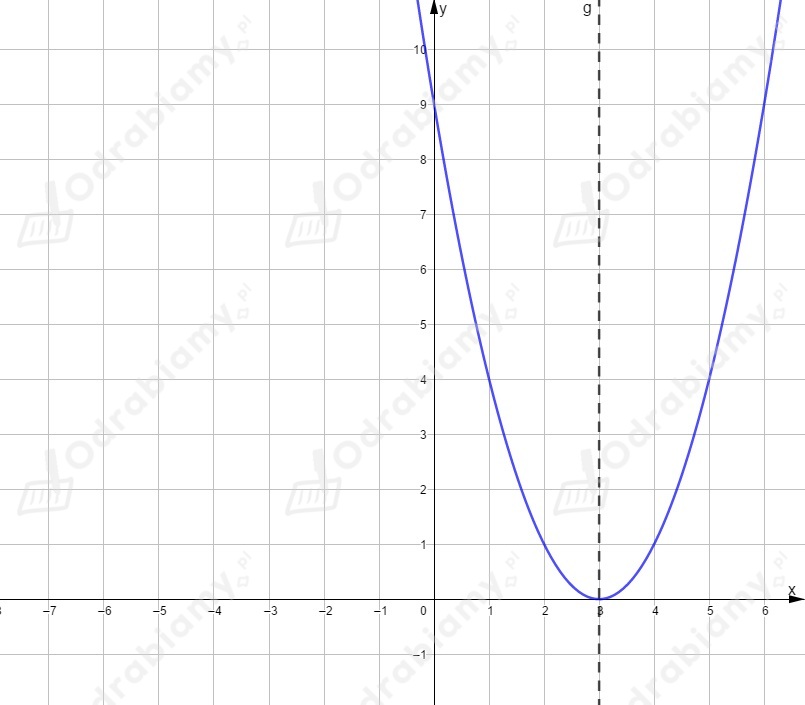
Jest to wykres funkcji     przesunięty o  jednostkę w prawo, czyli wektor  .

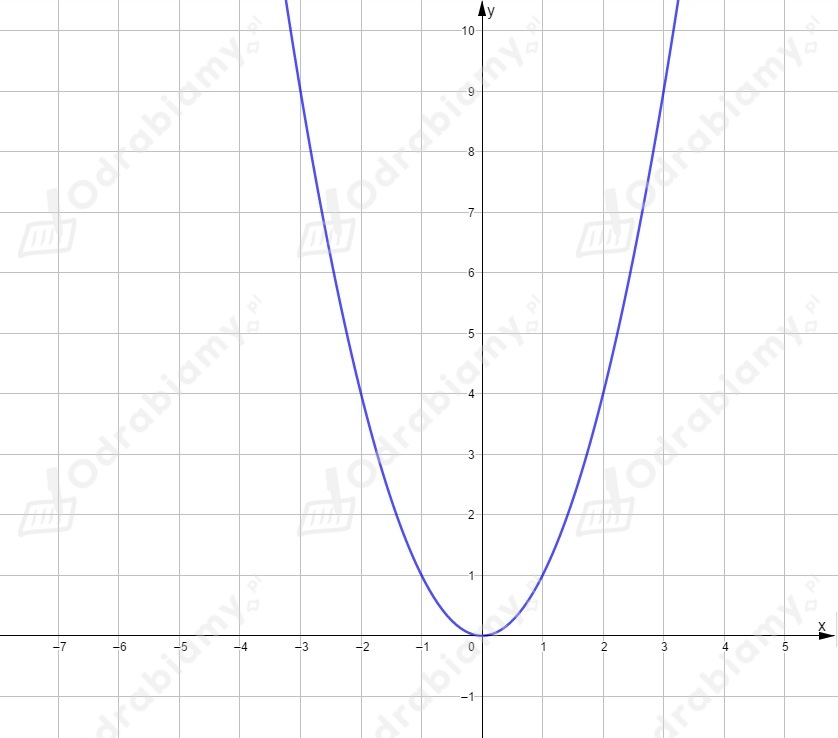
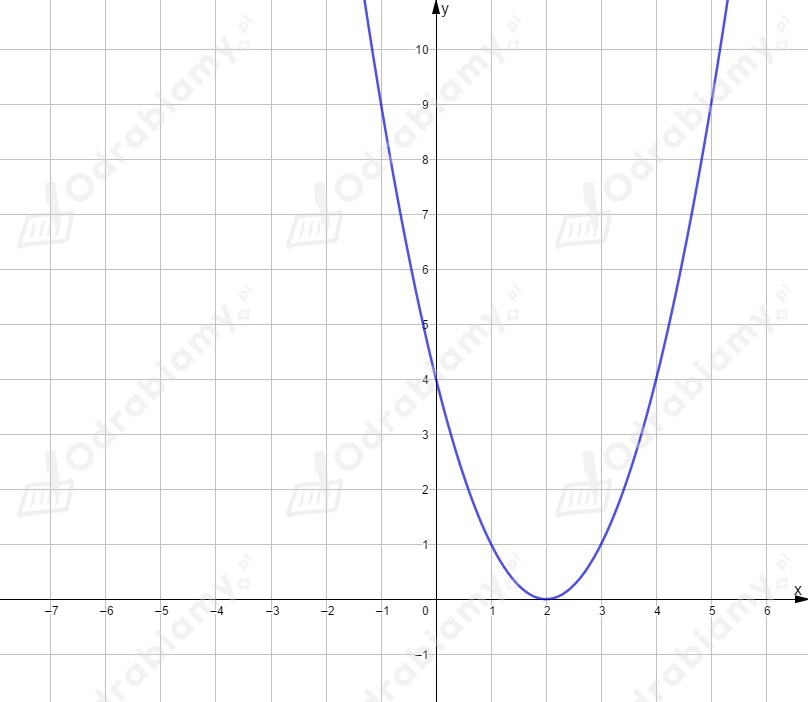
Po podstawieniu liczby  otrzymamy , czyli wykres przesunięty o wektor .

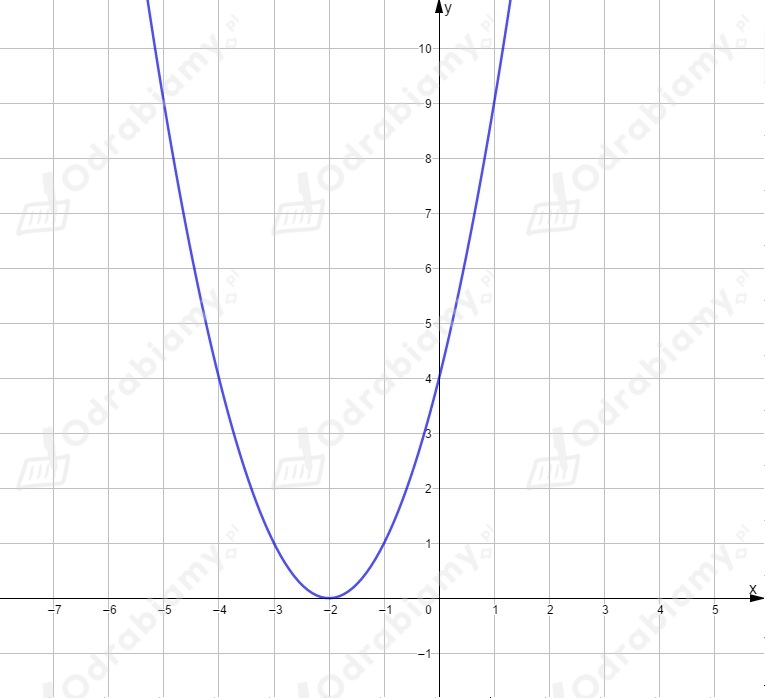
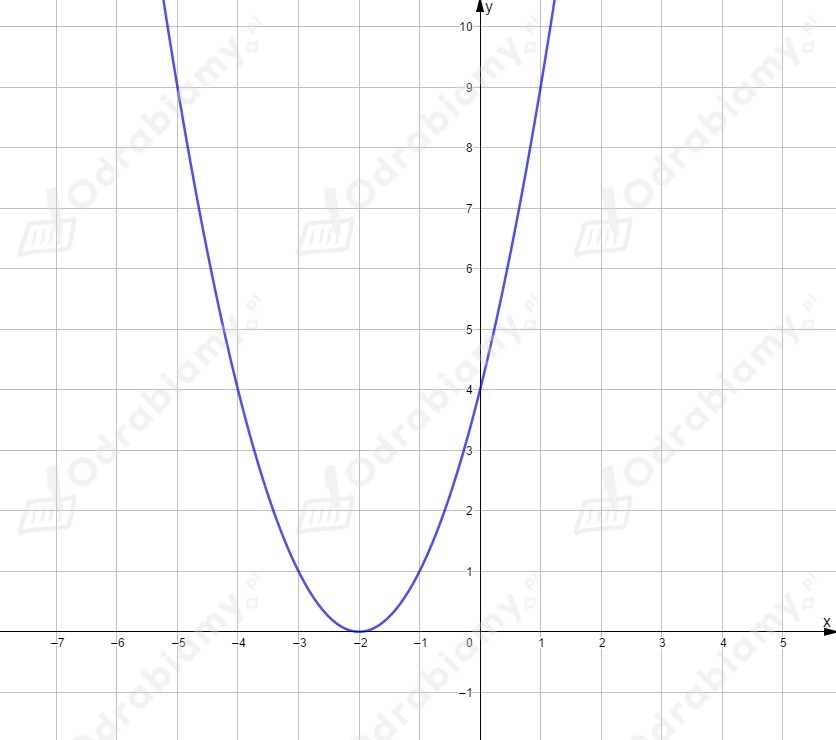
Dla  mamy wykres przesunięty o wektor .

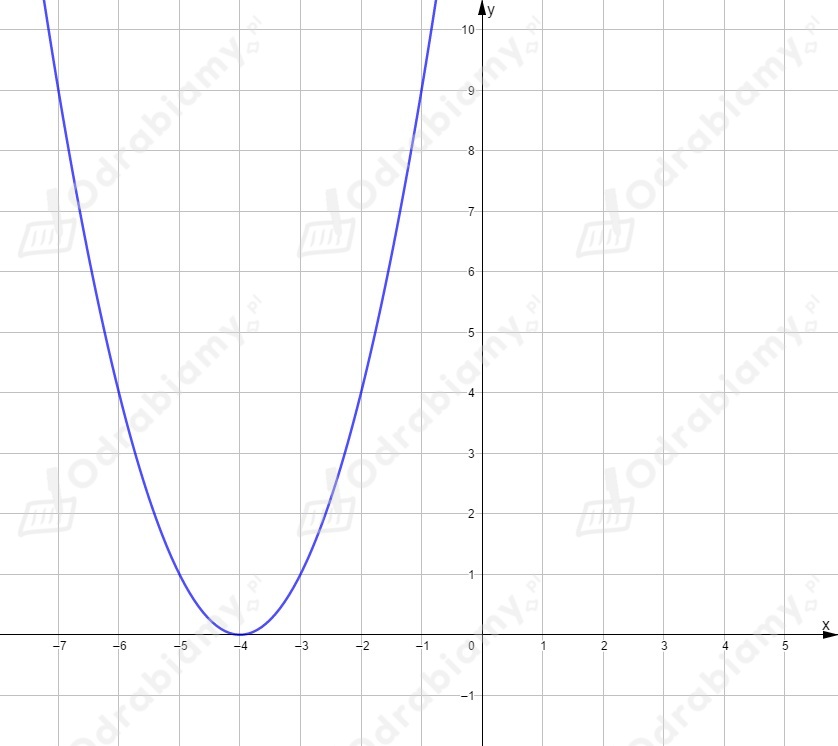
I ostatni przykład, dla  :  .

 Przypomnijmy, że wierzchołek paraboli danej wzorem   ma współrzędne .

Prosta   jest osią symetrii paraboli.

Po przekształceniu naszego wzoru   do postaci  ,

zauważymy, że aby osią symetrii paraboli była prosta   , to   musi być równe    

.

Podstawiając do podanego wzoru , otrzymamy wykres funkcji , 

której wierzchołek ma współrzędne  , zatem znajduje się na prostej   . 

  Aby wyznaczyć , wystarczy współrzędne punktu  podstawić do wzoru ,

ponieważ punkt ten ma należeć do wykresu tej funkcji.

,  .

Dla  mamy wykres przesunięty o wektor  dany wzorem .

I dla   wykres przesunięty o wektor  dany wzorem   .