Przypomnijmy, że wierzchołek paraboli danej wzorem  ma współrzędne .

  Funkcje   powstają w wyniku przesunięcia wykresu funkcji  wzdłuż osi  .  

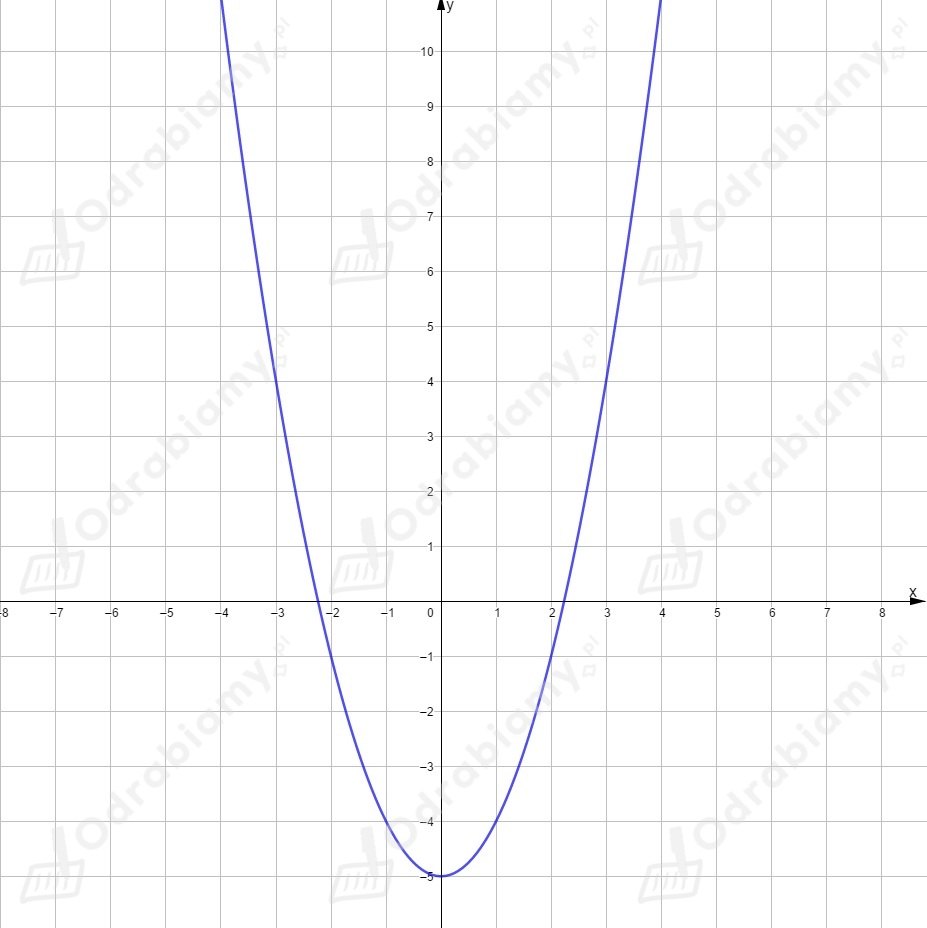
Dla   funkcja ma postać .

Powstała ona przez przesunięcie wykresu funkcji   o  jednostek w dół,

czyli o wektor . Wierzchołek ma współrzędne .  

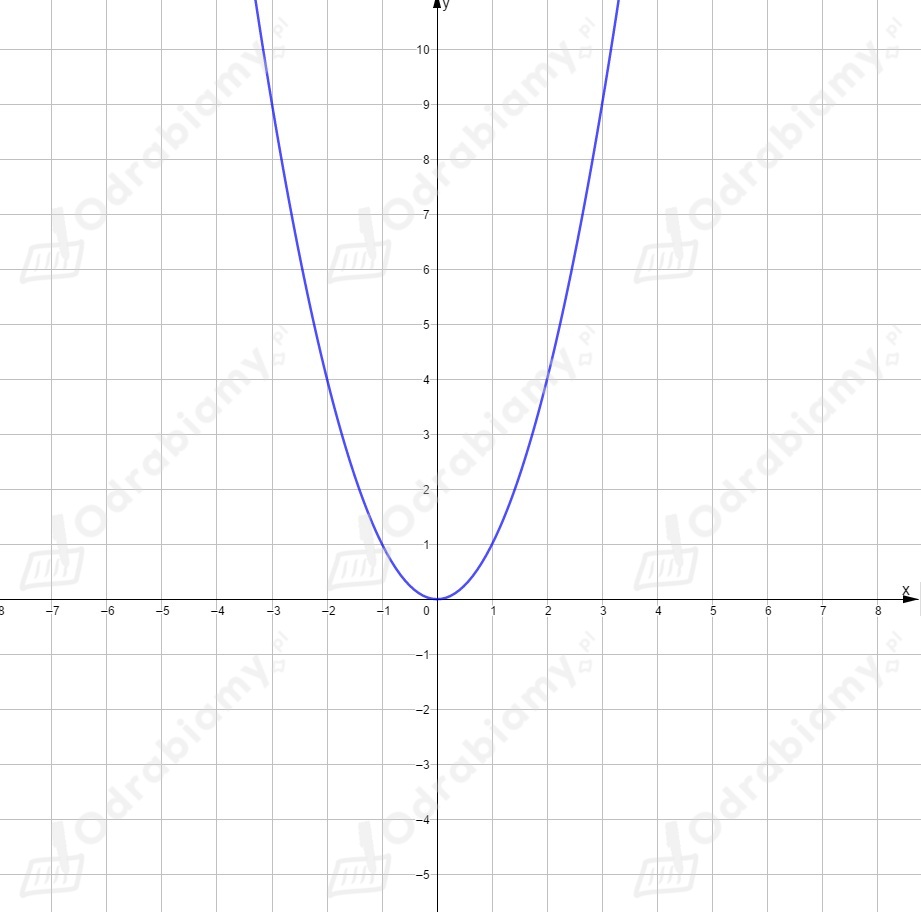
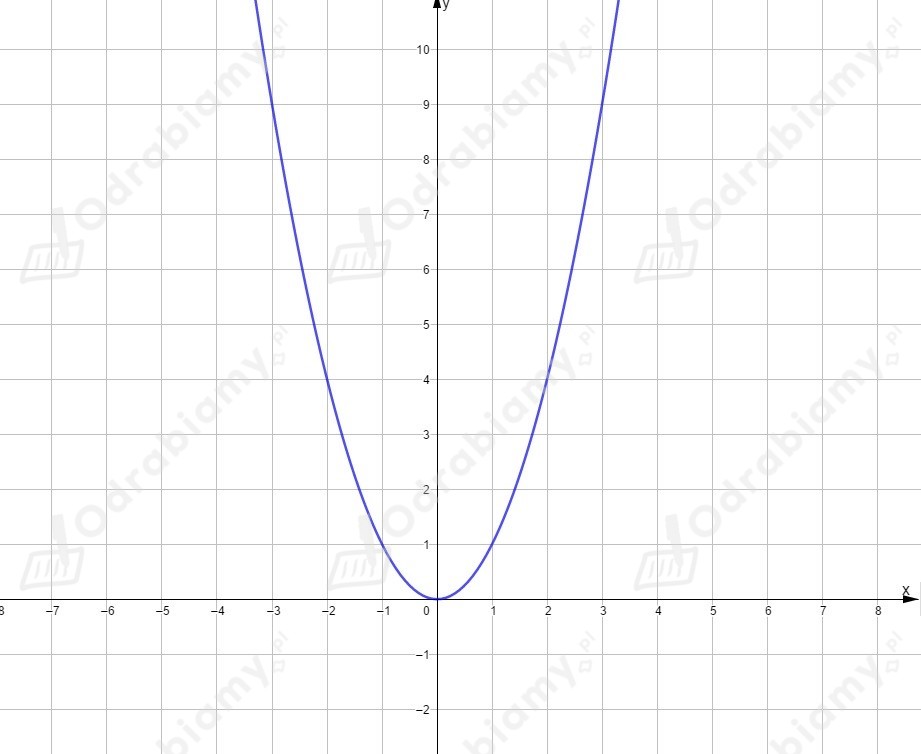
Dla   funkcja ma postać  . Wierzchołek ma współrzędne .  

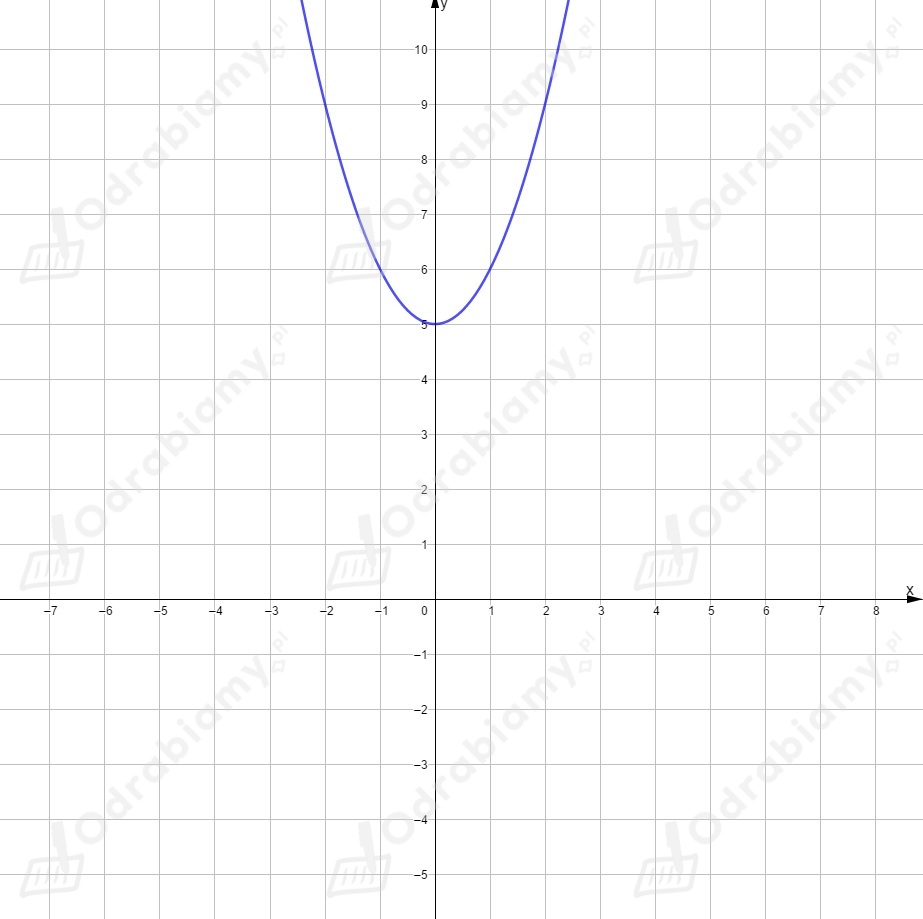
Dla   funkcja ma postać .

Powstała ona przez przesunięcie wykresu funkcji   o  jednostek w górę,

czyli o wektor  . Wierzchołek ma współrzędne .  

Możemy zauważyć, że wierzchołek funkcji  zawsze będzie leżał na prostej  .

  Funkcje   powstają w wyniku przesunięcia wykresu funkcji   wzdłuż osi  .   

Dla   funkcja ma postać  .

Powstała ona przez przesunięcie wykresu funkcji   o   jednostek w lewo,

czyli o wektor  . Wierzchołek ma współrzędne .  

Dla  funkcja ma postać  . Wierzchołek ma współrzędne .  

Dla   funkcja ma postać  .

Powstała ona przez przesunięcie wykresu funkcji   o   jednostek w prawo,

czyli o wektor  . Wierzchołek ma współrzędne .  

Możemy zauważyć, że wierzchołek funkcji  zawsze będzie leżał na prostej   .

  Funkcje   powstają w wyniku przesunięcia wykresu funkcji   

o  jednostki w prawo i o  jednostek wzdłuż osi , czyli o wektor .     

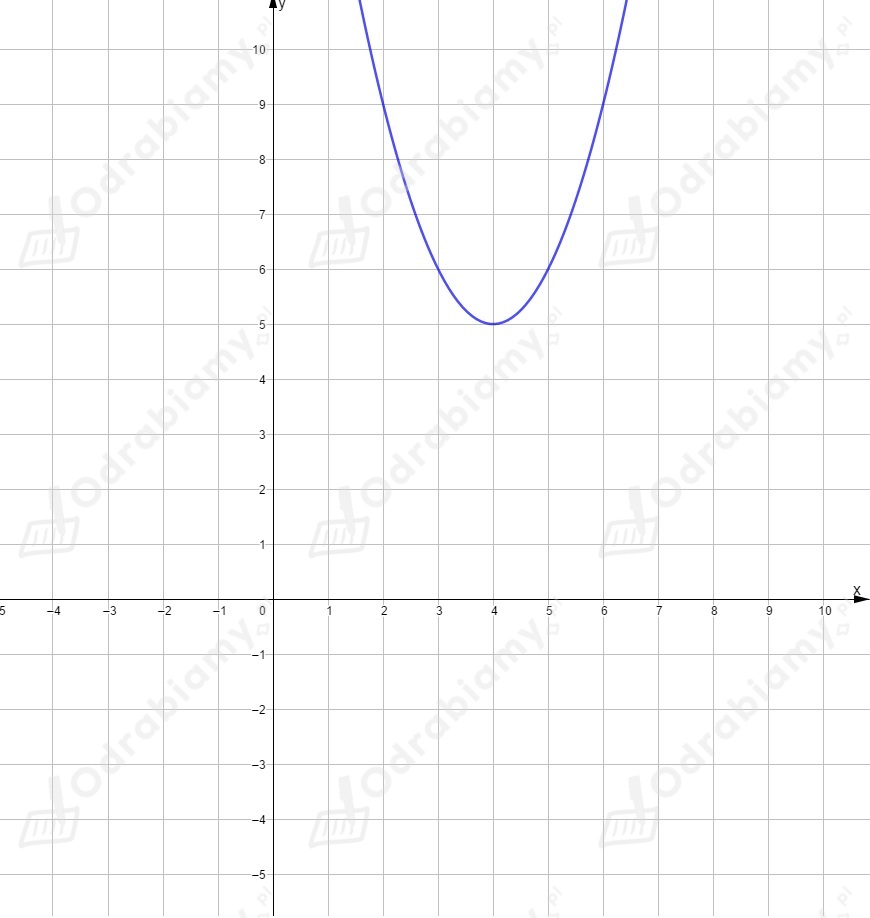
Dla   funkcja ma postać  .

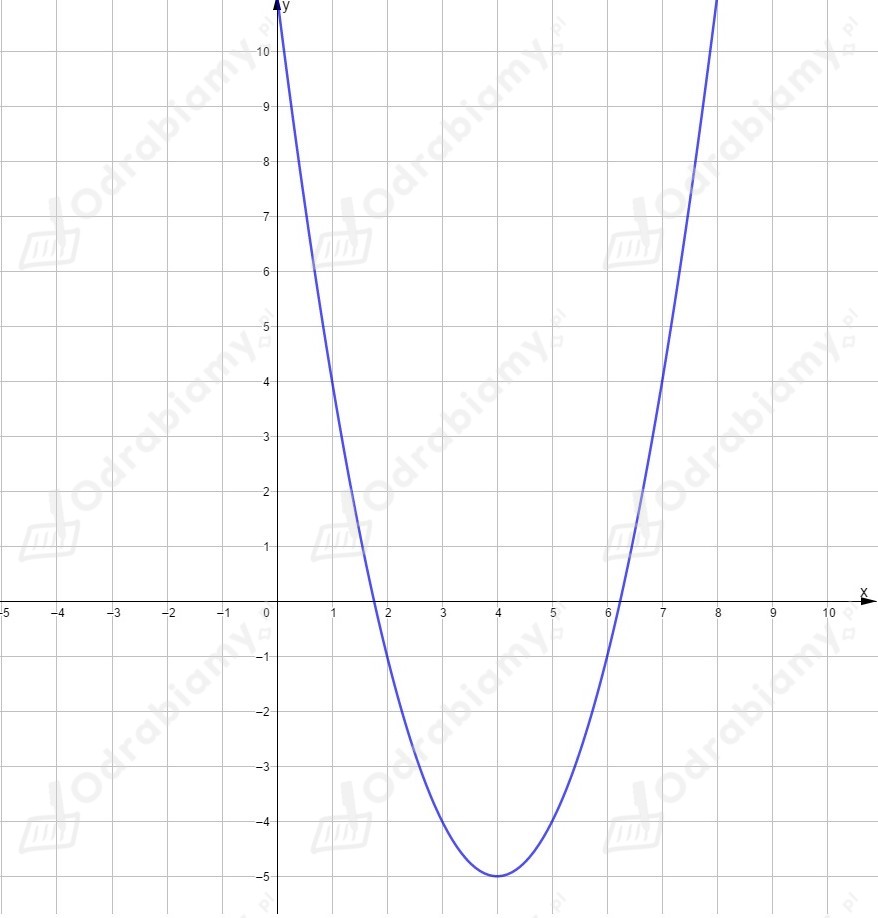
Powstała ona przez przesunięcie wykresu funkcji   o   jednostki w prawo i o   jednostek w dół, 

czyli o wektor  .  Wierzchołek ma współrzędne .  

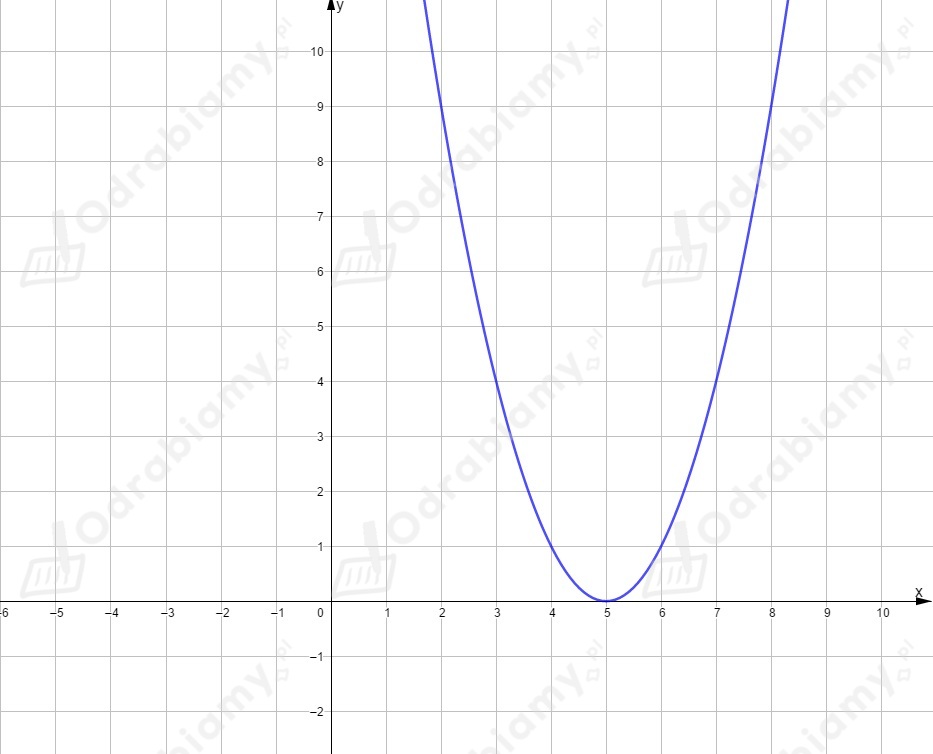
Dla   funkcja ma postać . 

Powstała ona przez przesunięcie wykresu funkcji   o   jednostki w prawo, 

czyli o wektor  . Wierzchołek ma współrzędne .  

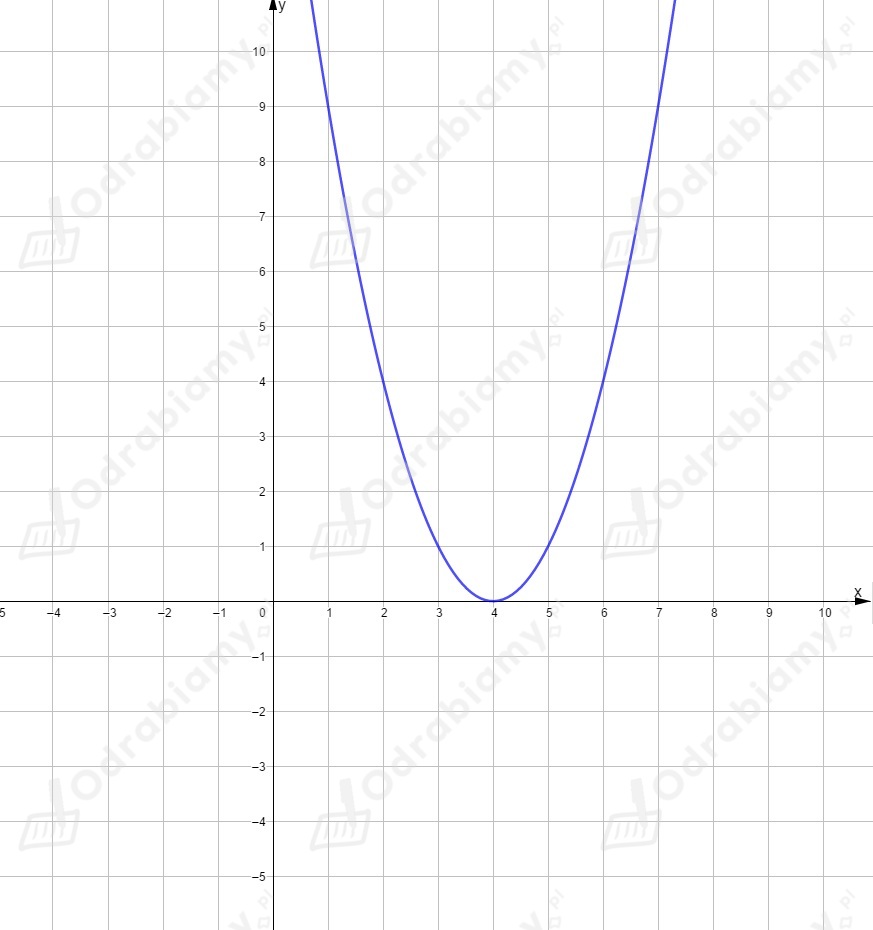
Dla   funkcja ma postać .

Powstała ona przez przesunięcie wykresu funkcji   o   jednostki w prawo i o   jednostek w górę, 

czyli o wektor  .  Wierzchołek ma współrzędne .  

Możemy zauważyć, że wierzchołek funkcji  zawsze będzie leżał na prostej  .

d) Funkcje   powstają w wyniku przesunięcia wykresu funkcji   

o  jednostek wzdłuż osi  i o  jednostek wzdłuż osi , czyli o wektor  .     

Dla   funkcja ma postać  .

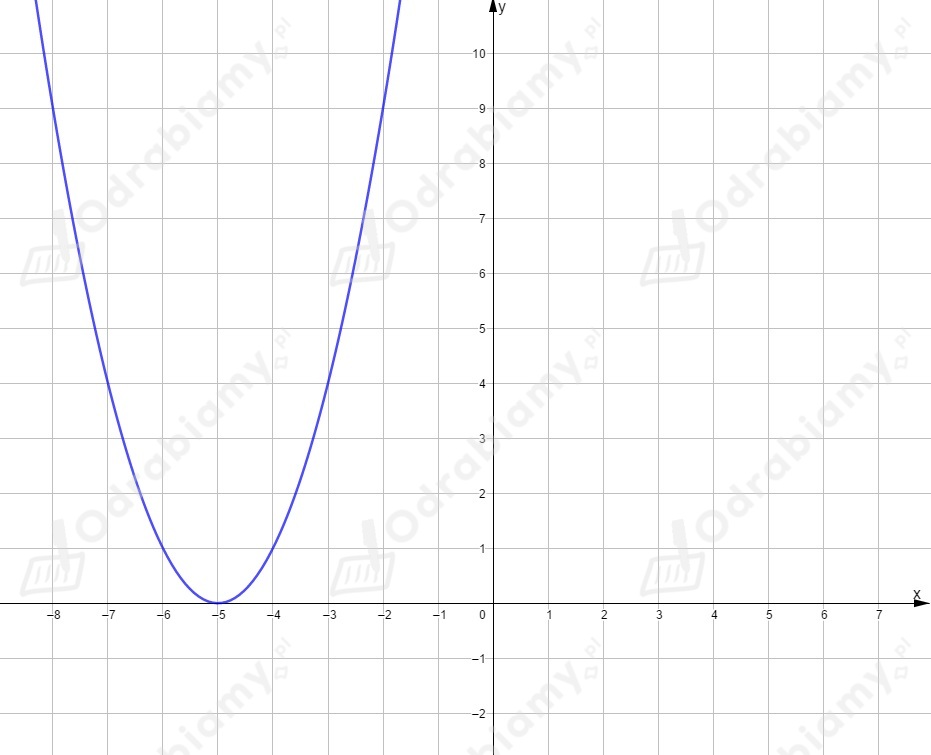
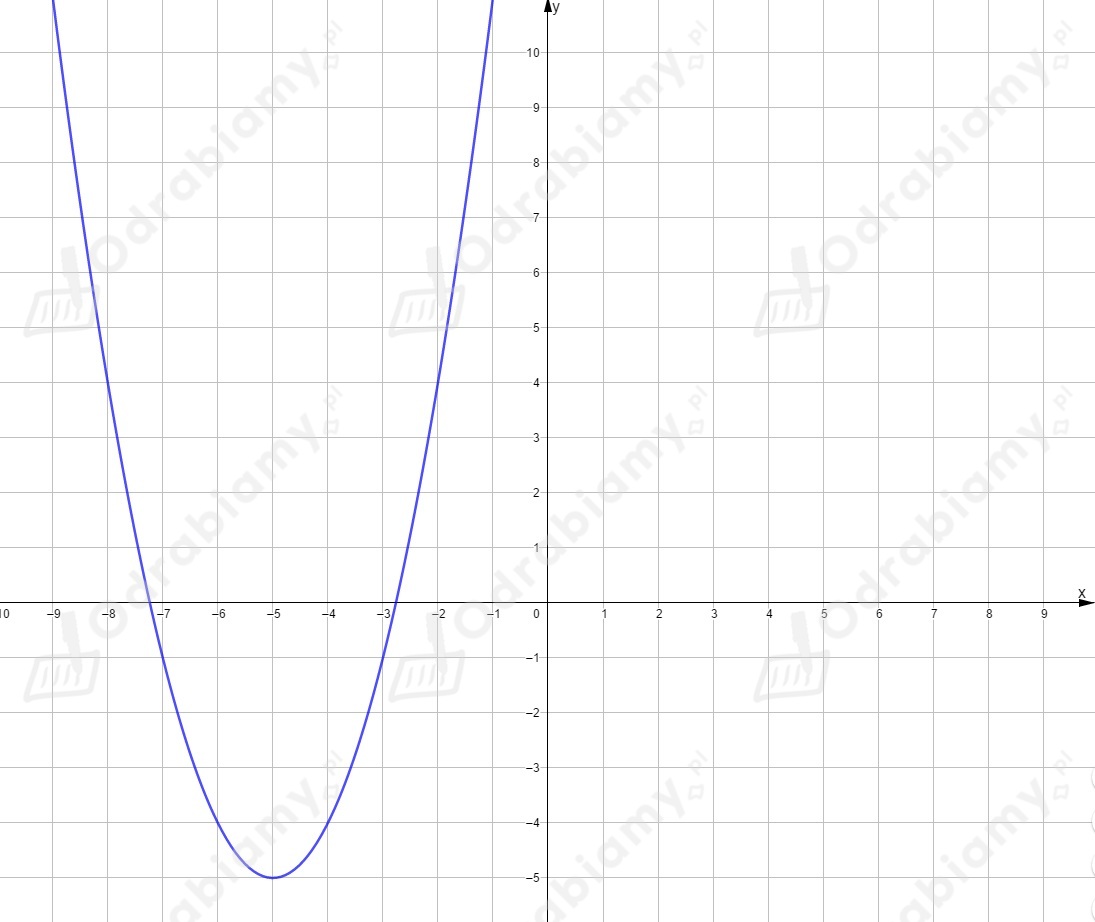
Powstała ona przez przesunięcie wykresu funkcji   o   jednostek w lewo i o   jednostek w dół, 

czyli o wektor  . Wierzchołek ma współrzędne .  

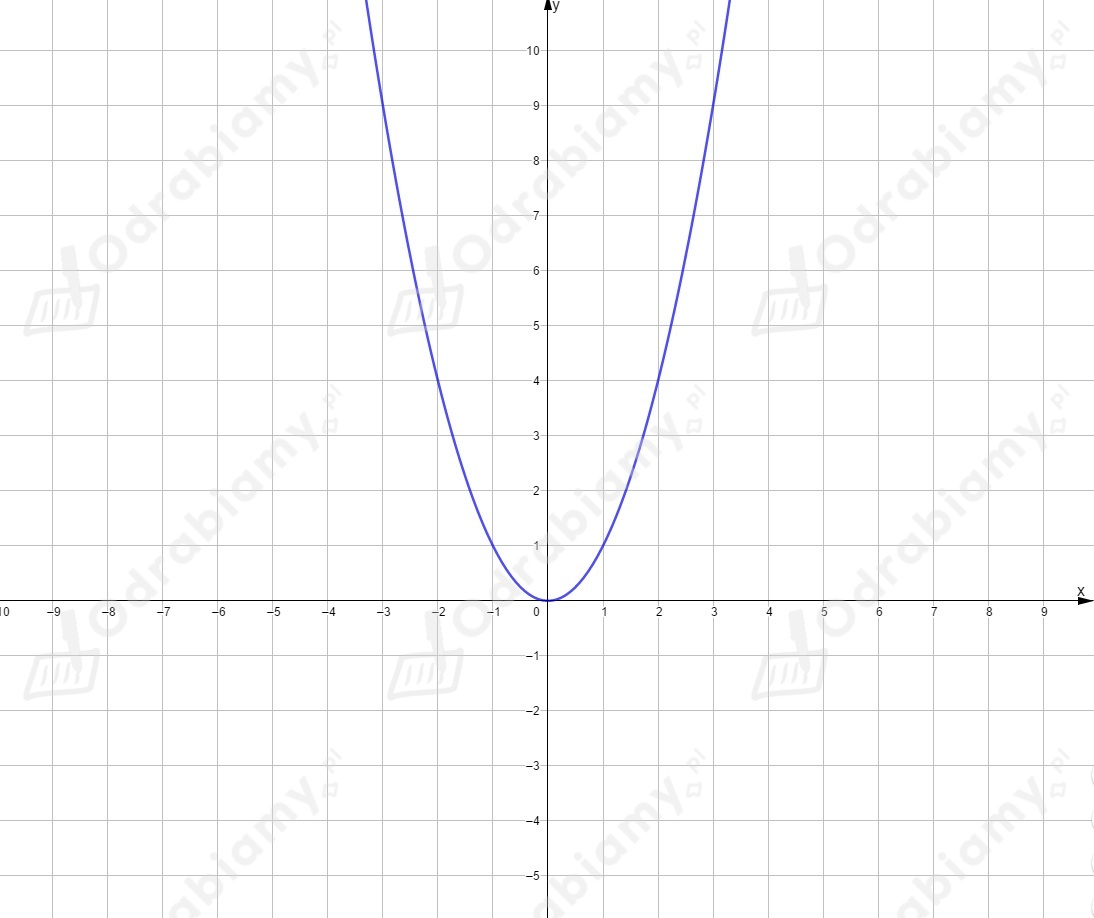
Dla   funkcja ma postać  . 

Wierzchołek ma współrzędne .  

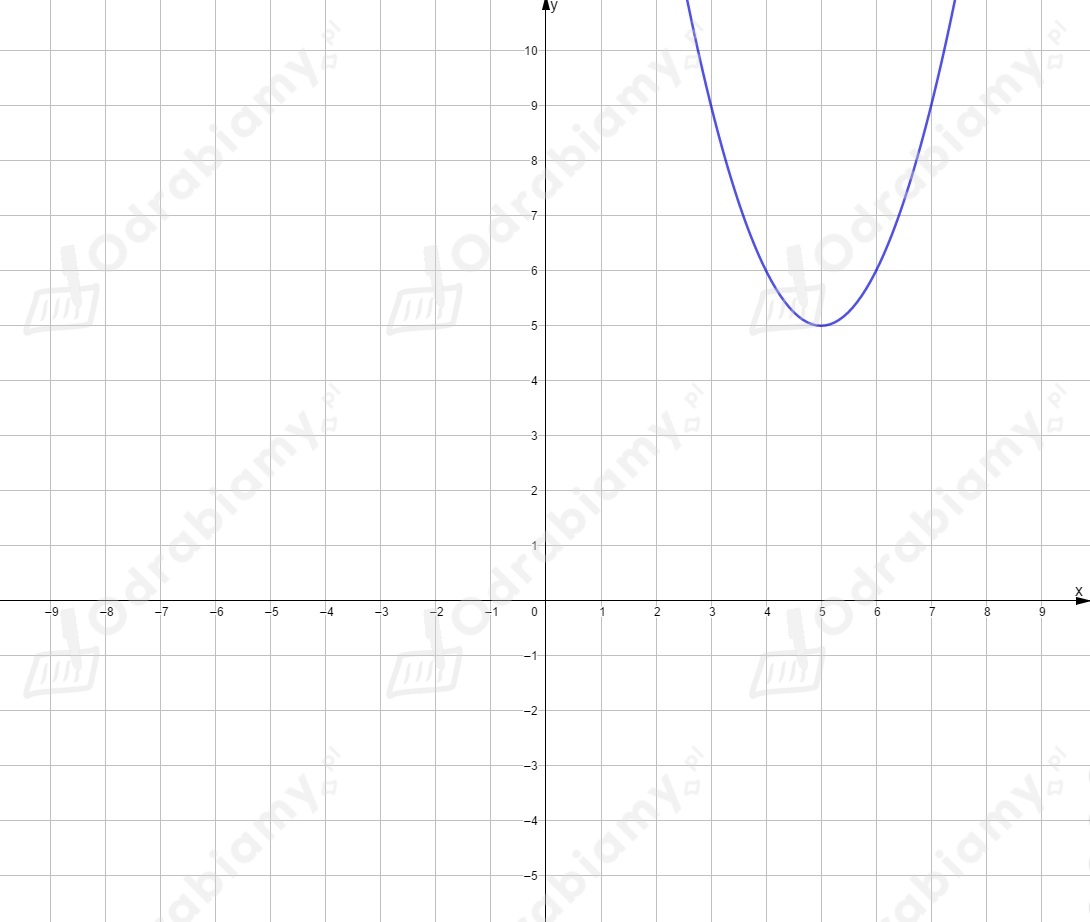
Dla   funkcja ma postać  .

Powstała ona przez przesunięcie wykresu funkcji   o   jednostek w prawo i o   jednostek w górę, 

czyli o wektor  . Wierzchołek ma współrzędne .  

Możemy zauważyć, że wierzchołek funkcji  zawsze będzie leżał na prostej  .