Jeśli przesuniemy wykres funkcji   o wektor    to otrzymamy funkcję:

.

Wykres funkcji  otrzymujemy przez odbicie wykresu funkcji  względem osi .

Wykresy  i  są symetryczne względem osi .

Wykres funkcji  otrzymujemy przez odbicie wykresu funkcji  względem osi .

Wykresy  i  są symetryczne względem osi .

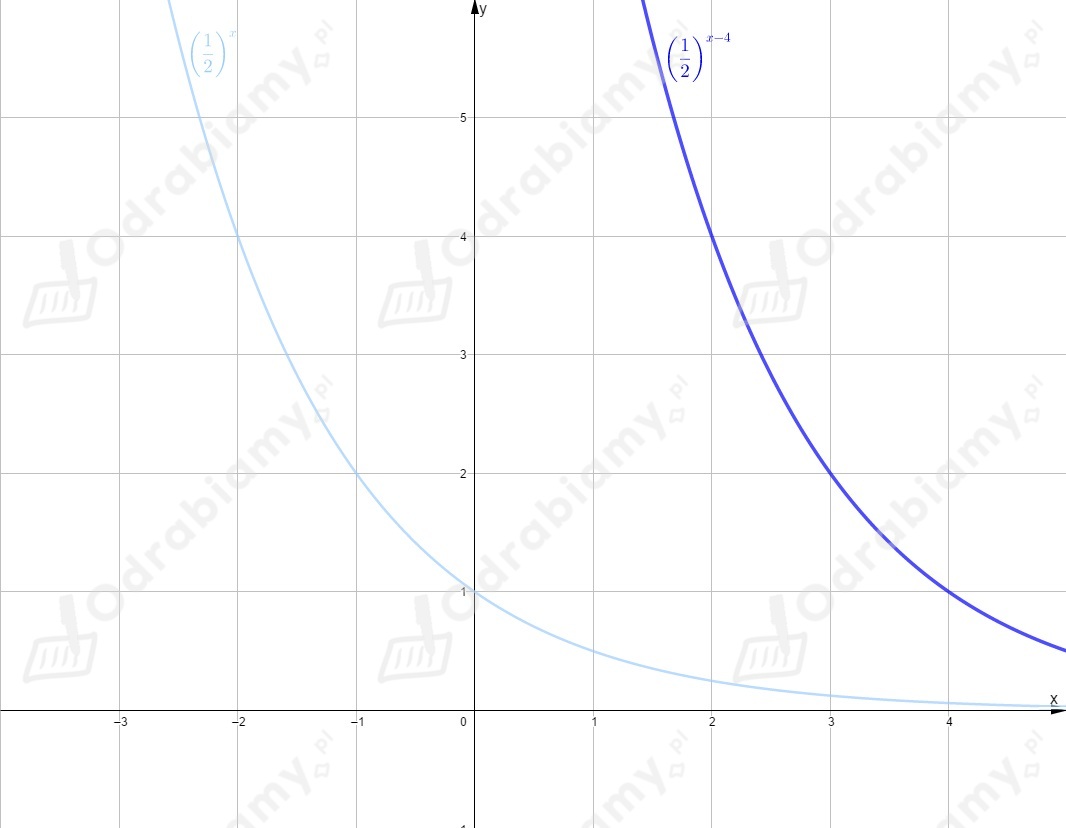
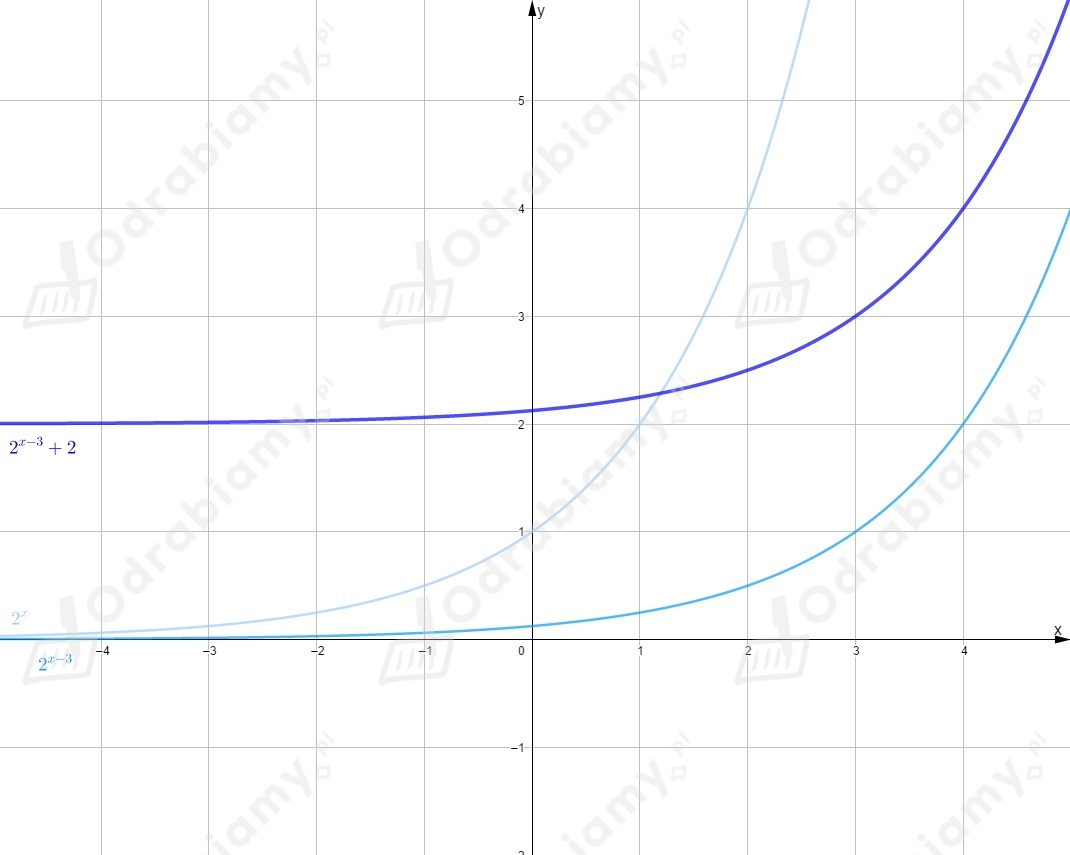
Rysujemy wykres funkcji  i przesuwamy go o  jednostki w prawo wzdłuż osi .

Rysujemy wykres funkcji .

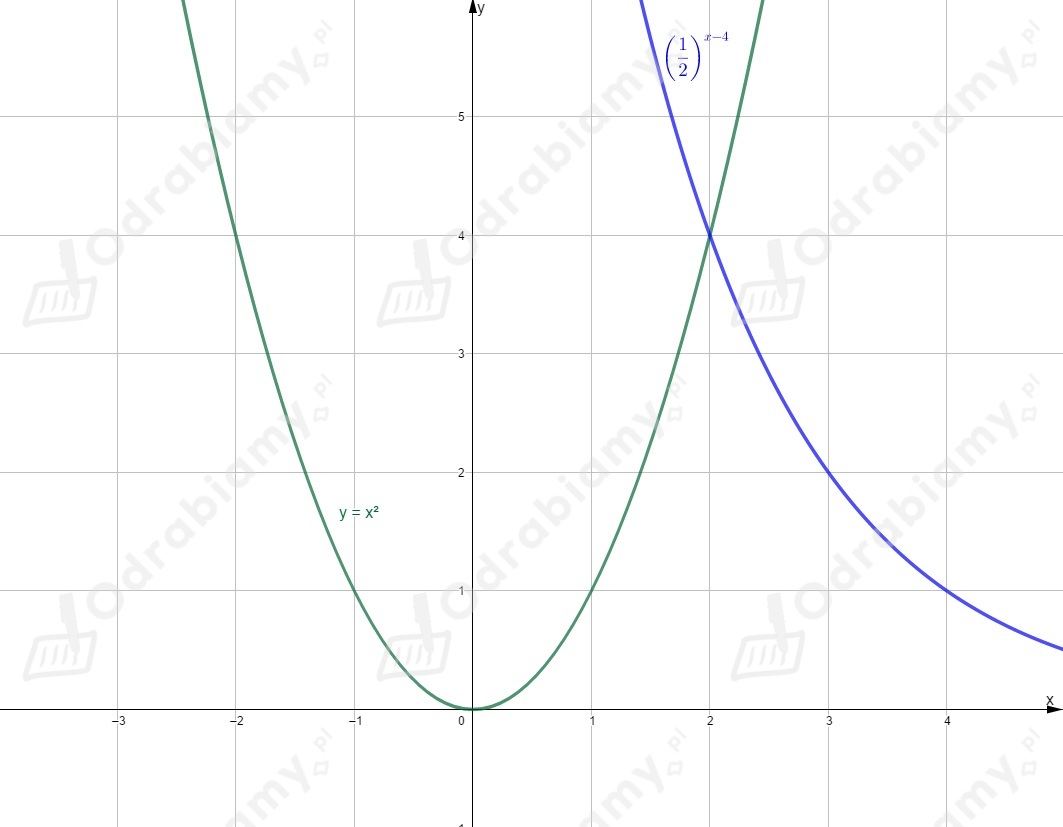
Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy rozwiązanie równania (punkt przecięcia wykresu funkcji  i wykresu funkcji ) 

 dla .

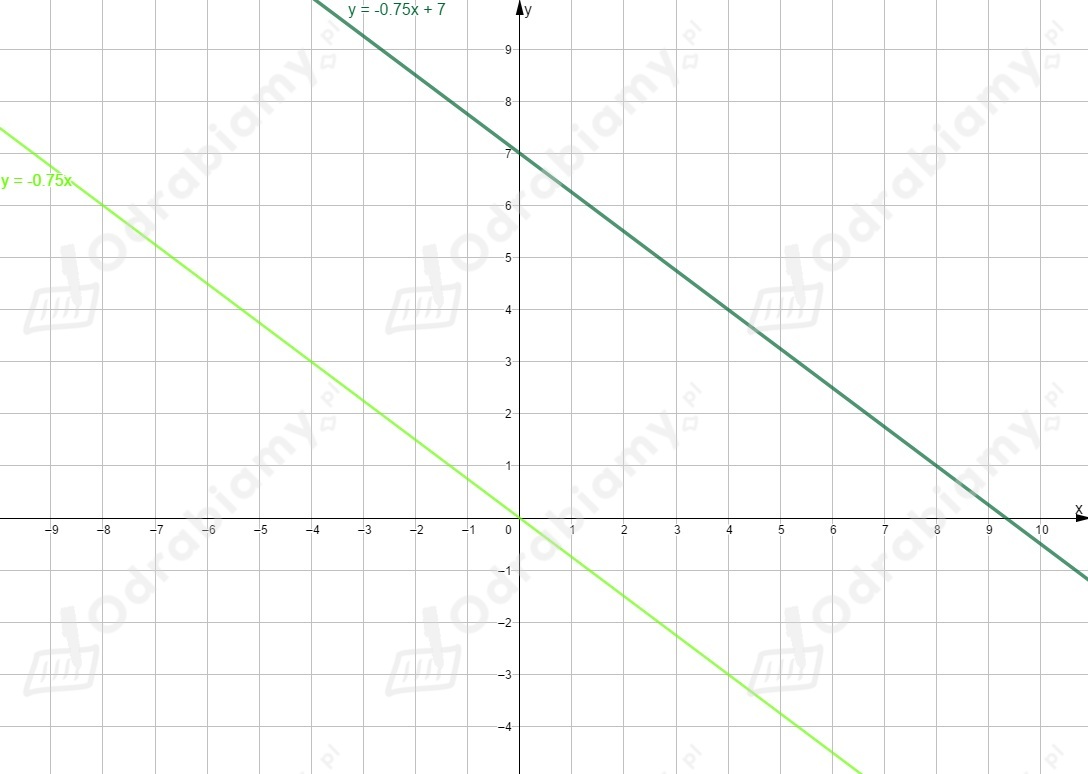
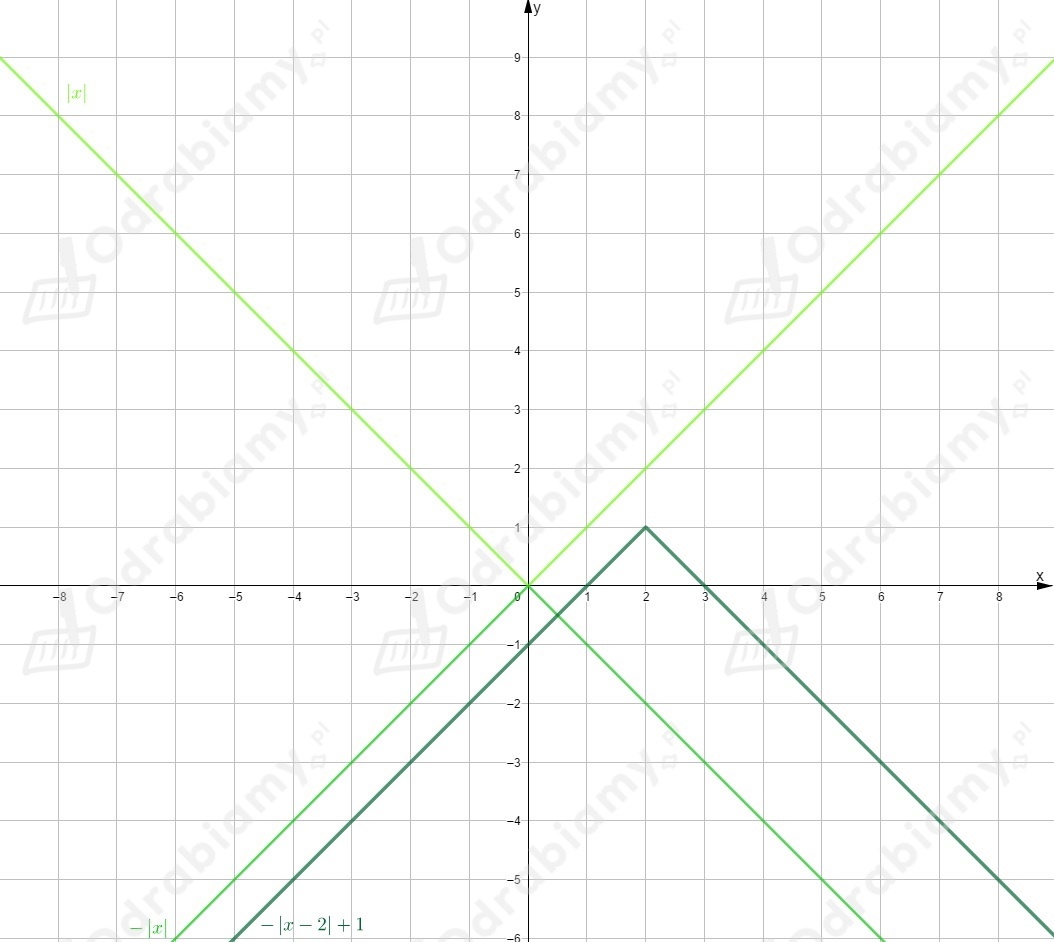
Rysujemy wykres funkcji   

Następnie wykres ten przesuwamy o   jednostki w lewo wzdłuż osi   

i o  jednostkę w dół wzdłuż osi .

Na koniec wykres funkcji  odbijamy symetrycznie względem osi  .

Otrzymujemy wykres funkcji o równaniu  .

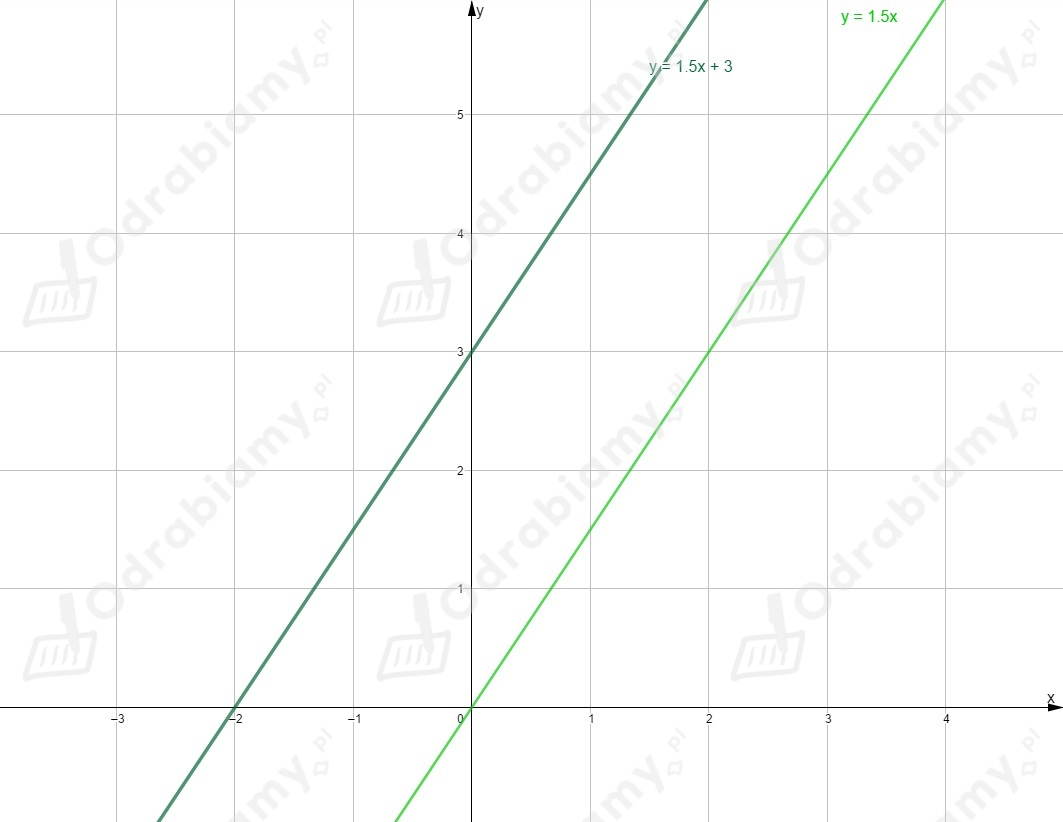
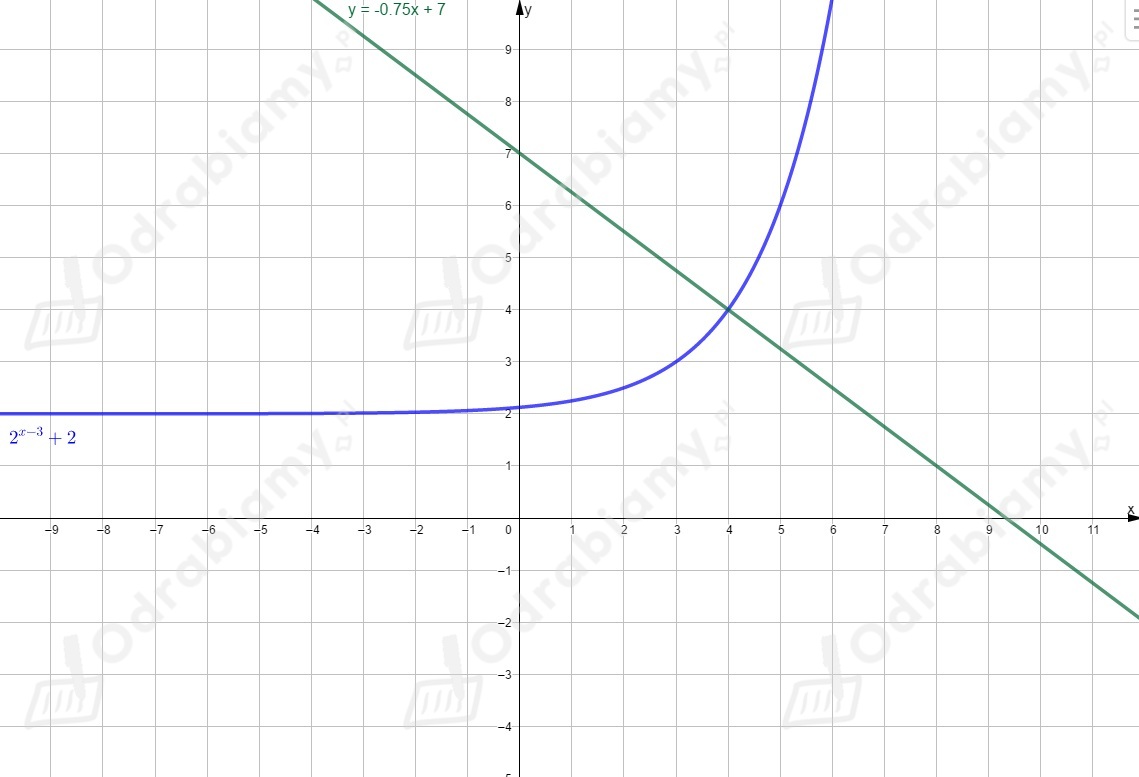
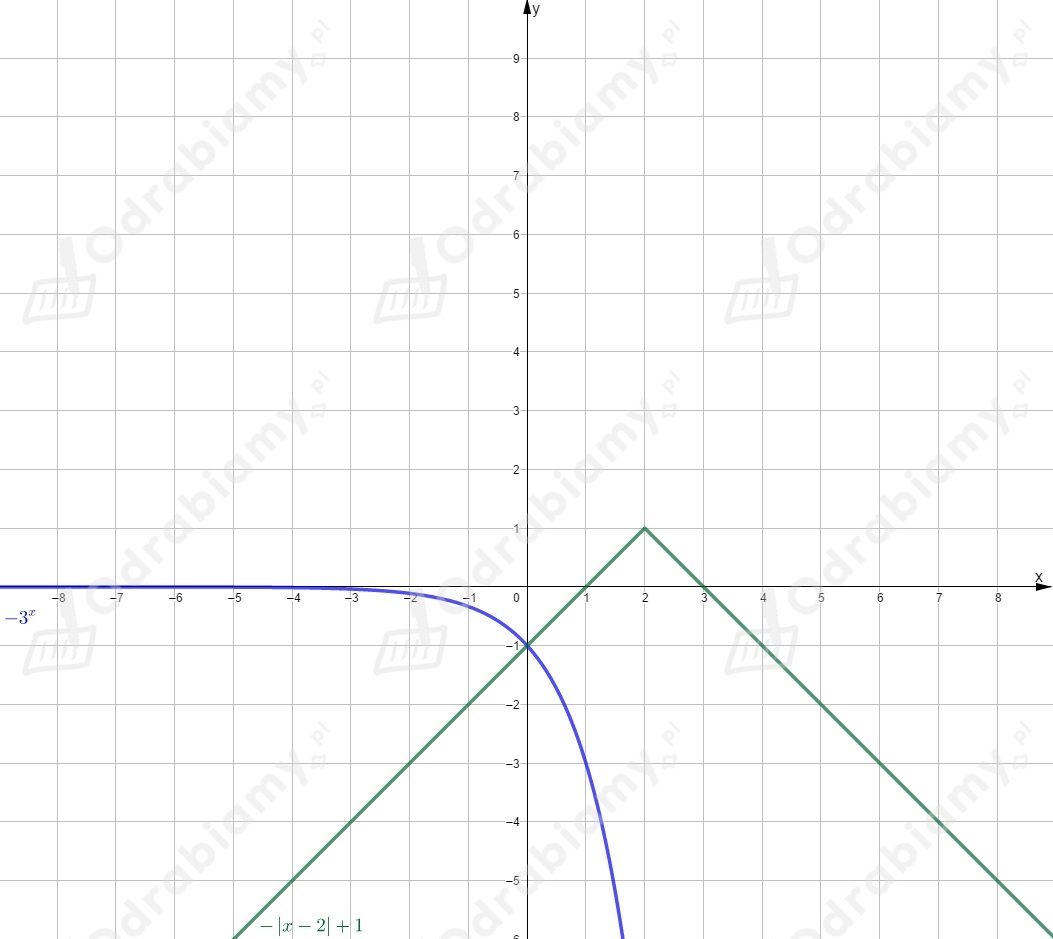
Rysujemy wykres funkcji   i przesuwamy go o  jednostki w górę wzdłuż osi .

Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy rozwiązanie równania (punkt przecięcia wykresu funkcji  i wykresu funkcji ) 

 dla .

Ze wzoru ogólnego funkcji   wyznaczamy  

Rysujemy wykres funkcji  i przesuwamy go o  jednostki w prawo wzdłuż osi

i o  jednostki w górę wzdłuż osi .

Ze wzoru ogólnego funkcji   wyznaczamy  

.

Rysujemy wykres funkcji  i przesuwamy go o  jednostek w górę wzdłuż osi .

Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy rozwiązanie równania (punkt przecięcia wykresu funkcji  i wykresu funkcji ) 

 dla  .

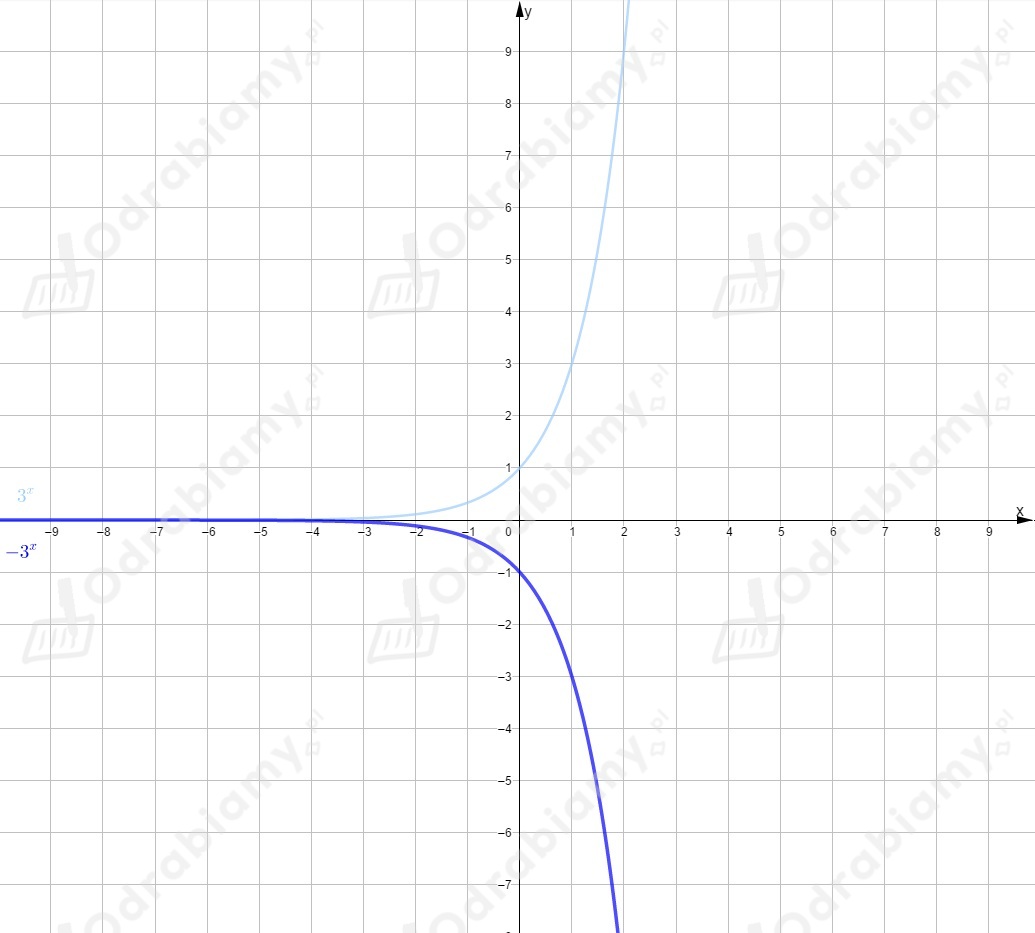
Rysujemy wykres funkcji  i odbijamy go symetrycznie względem osi  .

Rysujemy wykres funkcji  i odbijamy go symetrycznie względem osi .

Otrzymujemy wykres funkcji o równaniu .

Następnie wykres przesuwamy o  jednostki w prawo wzdłuż osi   

i o  jednostkę w górę wzdłuż osi .

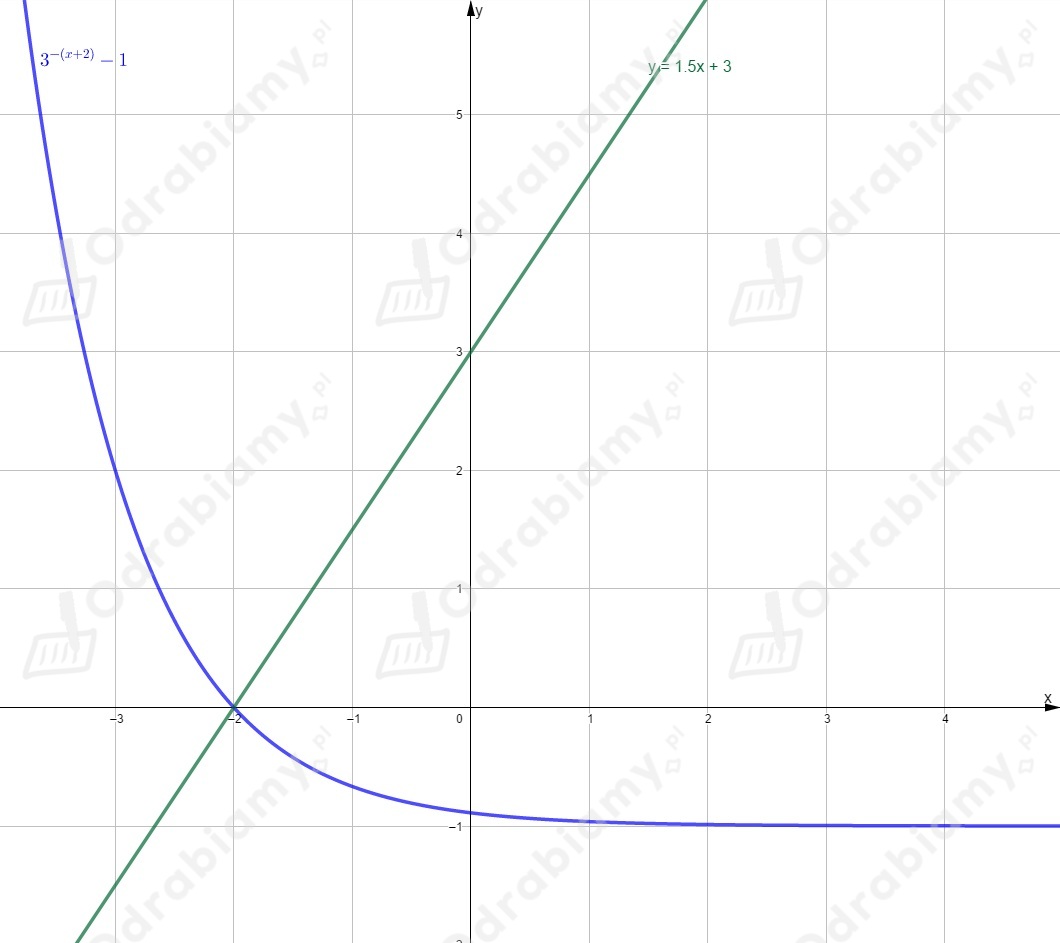
Rysujemy oba wykresy w jednym układzie współrzędnych.

Odczytujemy rozwiązanie równania (punkt przecięcia wykresu funkcji  i wykresu funkcji ) 

 dla .