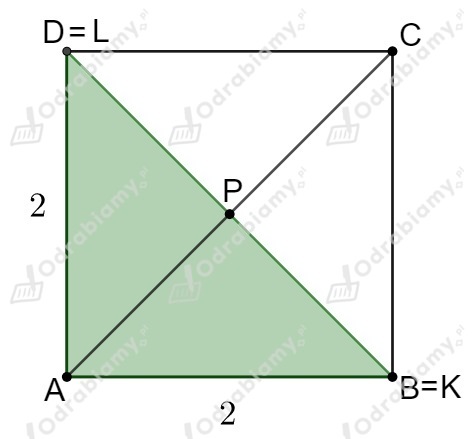
Odpowiedź:
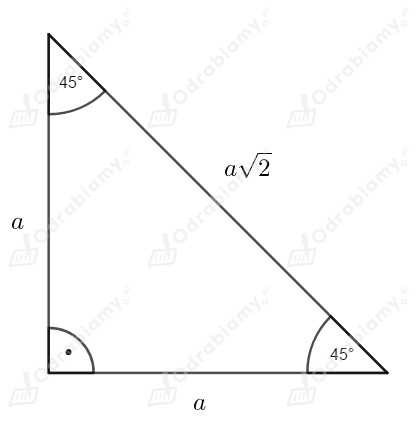
W trójkącie prostokątnym równoramiennym o przyprostokątnych długości ,
przeciwprostokątna ma długość .
Stosując twierdzenie Pitagorasa otrzymujemy:
Wykorzystujemy powyższe informacje dla trójkąta i obliczamy długość przekątnej
Przekątna ma długość .
Zauważmy, że możliwe są dwa przypadki ułożenia tego trójkąta:
1. Punkty i leżą na bokach i
Taka sytuacja będzie miała miejsce, gdy wysokość trójkąta będzie krótsza od połowy
długości przekątnej tego kwadratu, czyli .
Nie możemy rozważać przypadku gdy , ponieważ wtedy punkty i pokryją się z punktem .
Rozumowanie nie zmieni się gdy będzie równe (musimy rozważyć wszystkie możliwe przypadki), dlatego bierzemy pod uwagę
.
2. Punkty i leżą na bokach i
Będzie tak dla .
Przedział jest lewostronnie otwarty, ponieważ zdarzenie, gdy zawarte jest w przypadku 1.
i prawostronnie otwarty, ponieważ gdyby było równe , to punkty i pokryłyby się z punktem .
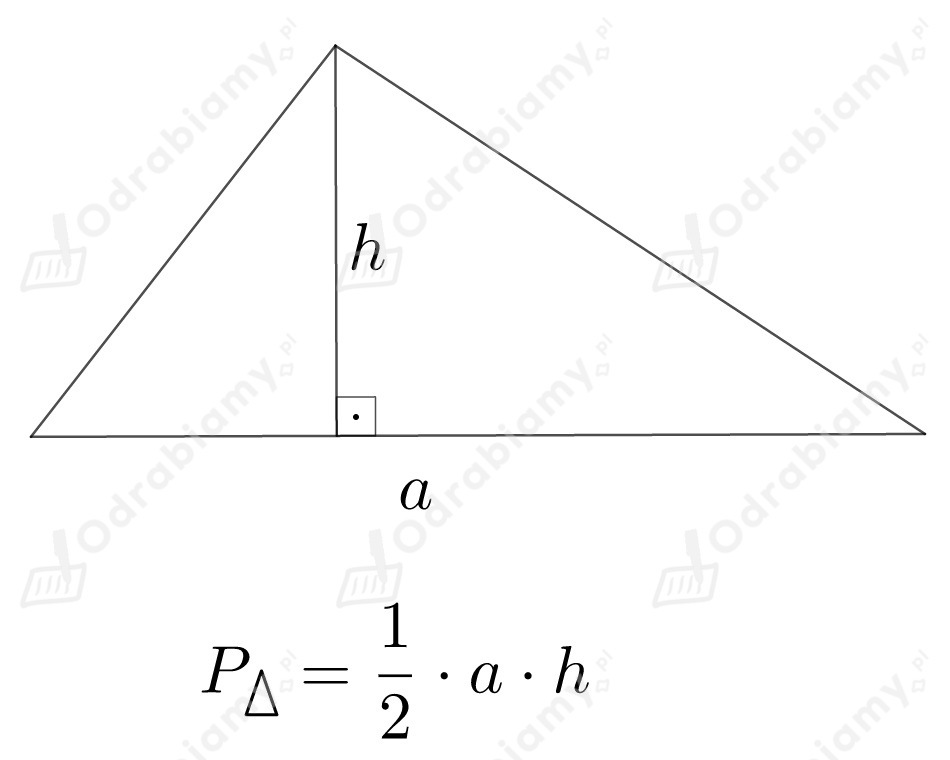
Przypomnijmy, że pole trójkąta o boku długości i wysokości opuszczonej na ten bok obliczamy ze wzoru:
Przypadek 1.
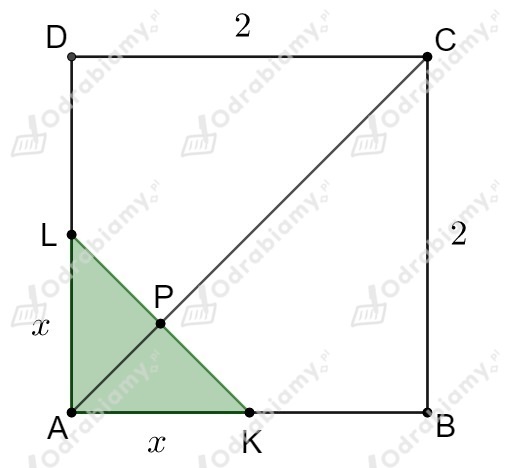
Do obliczenia pola trójkąta o wysokości potrzebna nam będzie długość jego podstawy .
Wiemy, że trójkąt jest równoramienny i jego wysokość zawarta jest w przekątnej .
Trójkąt jest przystający (taki sam) do trójkąta - trójkąty te są równoramienne i prostokątne
(ich kąty mają miary , , , bo każdy kąt w kwadracie ma , przekątna dzieli kąt
na dwa kąty, które mają po , a odcinek jest prostopadły do przekątnej ,
dlatego kąty i są proste).
Wiemy też, że odcinek jest wysokością trójkąta, czyli
.
Zatem .
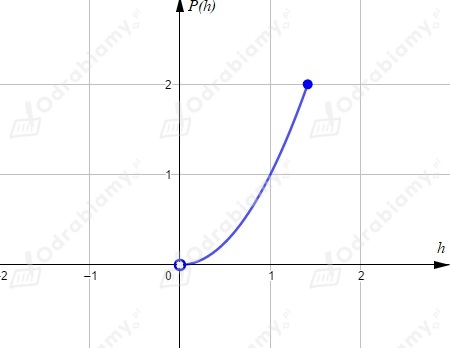
Pole trójkąta jako funkcja wysokości
Rysujemy wykres funkcji , pamiętając, ze przedział jest jej dziedziną.
Obliczmy wartości dla kilku argumentów:
(punkt ten nie należy do dziedziny, dlatego zostawimy niezamalowane kółeczko)
Dla funkcja przyjmuje wartość największą.
Przypadek 2.
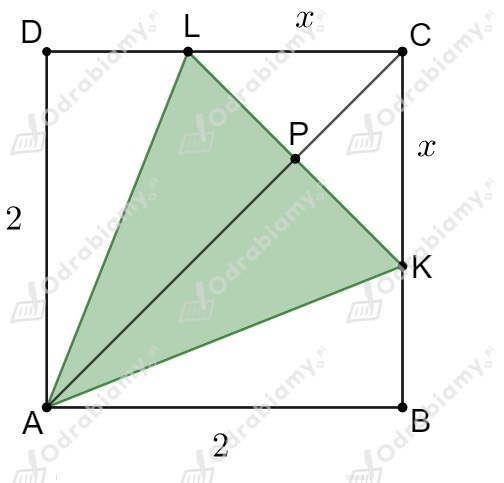
Do obliczenia pola trójkąta o wysokości potrzebna nam będzie długość jego podstawy .
Wiemy, że trójkąt jest równoramienny i jego wysokość zawarta jest w przekątnej .
Trójkąt jest przystający do trójkąta - trójkąty te są równoramienne i prostokątne
(ich kąty mają miary , , , bo każdy kąt w kwadracie ma , przekątna dzieli kąt
na dwa kąty, które mają po , a odcinek jest prostopadły do przekątnej ,
dlatego kąty i są proste).
.
Wiemy już, że długość połowy podstawy trójkąta jest równa długości odcinka .
.
Długość całej podstawy trójkąta wynosi
.
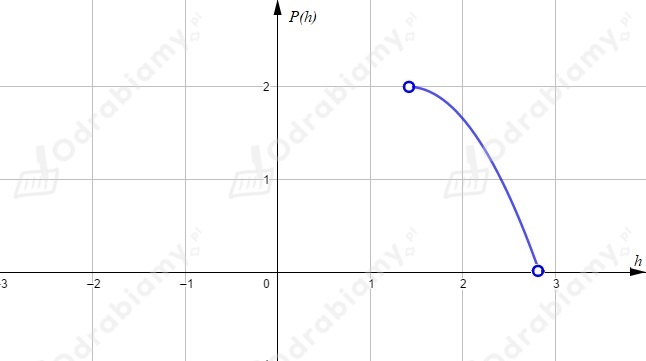
Pole trójkąta jako funkcja wysokości
Aby narysować wykres funkcji, obliczmy wartości dla kilku argumentów:
Ramiona paraboli skierowane są do dołu, ponieważ współczynnik przy najwyższej potędze jest ujemny.
Funkcja nie przyjmuje w swojej dziedzinie wartości największej
Największe pole dla .
Jest tak w przypadku, gdy punkty i pokrywają się z punktami i .