Obliczamy wartości funkcji w kilku punktach, aby narysować wykres

lub obliczamy wielkości przydatne przy rysowaniu paraboli

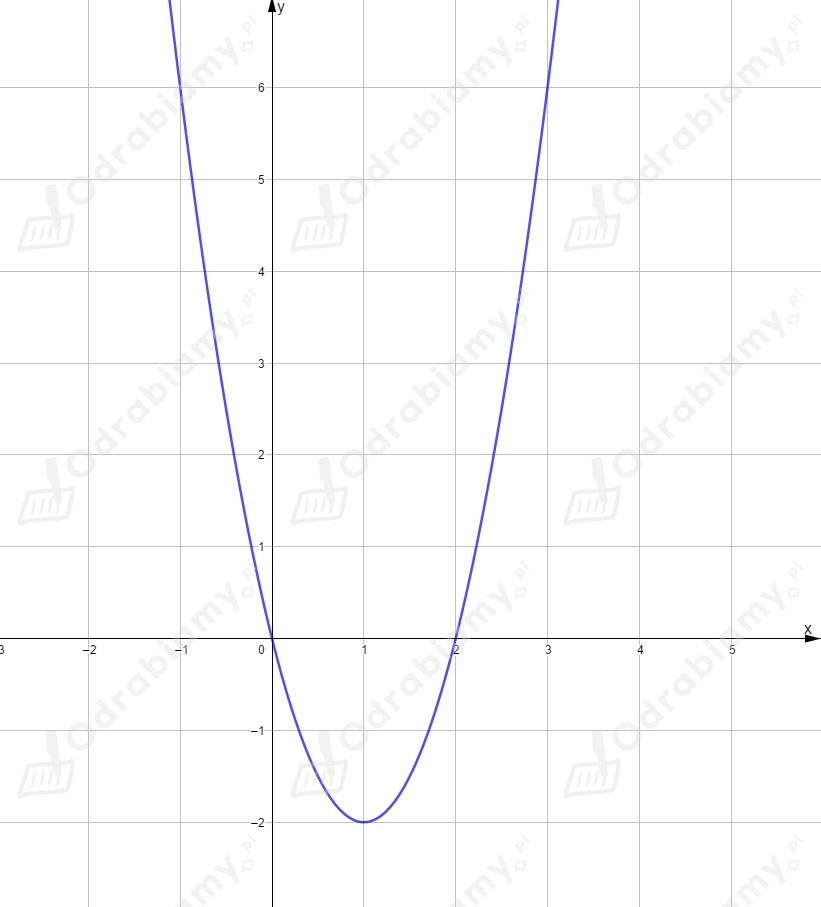
miejsca zerowe:

 lub   

,  , 

współrzędne wierzchołka:

,

współrzędne punktu przecięcia z osią 

.

Własności funkcji:

dziedziną jest zbiór   ,

zbiorem wartości jest przedział   , 

funkcja przyjmuje wartość najmniejszą równą  dla  i nie przyjmuje wartości największej,

miejscami zerowymi funkcji są argumenty  i ,

 dla ,  dla ,

osią symetrii wykresu jest prosta ,

funkcja jest malejąca w przedziale   ,
funkcja jest rosnąca w przedziale ,

równanie     
dla  nie ma rozwiązań,
dla  ma jedno rozwiązanie,
dla  ma dwa rozwiązania. 

Obliczamy wielkości przydatne przy rysowaniu paraboli

miejsca zerowe:

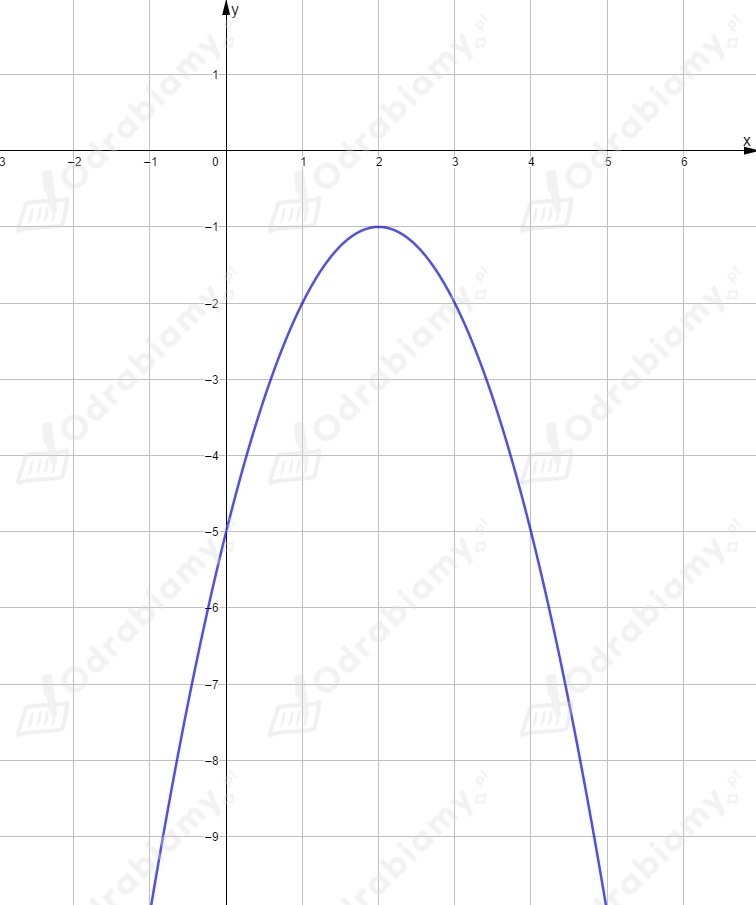
brak miejsc zerowych,

współrzędne wierzchołka:

,

współrzędne punktu przecięcia z osią 

.

Własności funkcji:

dziedziną jest zbiór , 

zbiorem wartości jest przedział ,  

funkcja przyjmuje wartość największą równą  dla  i nie przyjmuje wartości najmniejszej,

funkcja nie ma miejsc zerowych ,

 dla  ,

osią symetrii wykresu jest prosta  ,

funkcja jest rosnąca w przedziale   ,
funkcja jest malejąca w przedziale ,

równanie     
dla  ma dwa rozwiązania,
dla  ma jedno rozwiązanie,
dla  nie ma rozwiązań.

Obliczamy wielkości przydatne przy rysowaniu paraboli

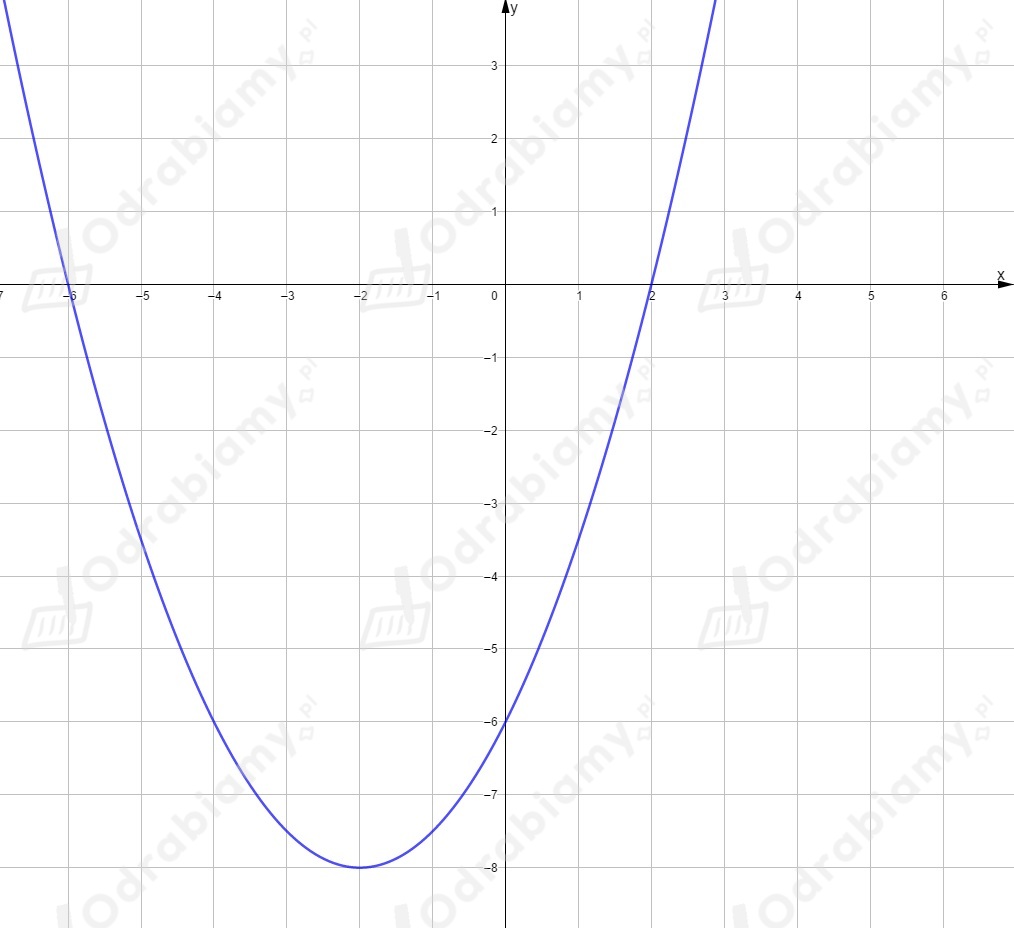
miejsca zerowe:

, ,

współrzędne wierzchołka:

,

współrzędne punktu przecięcia z osią 

.

Własności funkcji:

dziedziną jest zbiór , 

zbiorem wartości jest przedział ,  

funkcja przyjmuje wartość najmniejszą równą  dla  i nie przyjmuje wartości największej,

miejscami zerowymi funkcji są argumenty  i  ,

dla ,  dla , 

osią symetrii wykresu jest prosta  ,

funkcja jest malejąca w przedziale   ,    
funkcja jest rosnąca w przedziale ,

równanie     

dla  nie ma rozwiązań,
dla  ma jedno rozwiązanie,
dla  ma dwa rozwiązania.

Obliczamy wielkości przydatne przy rysowaniu paraboli

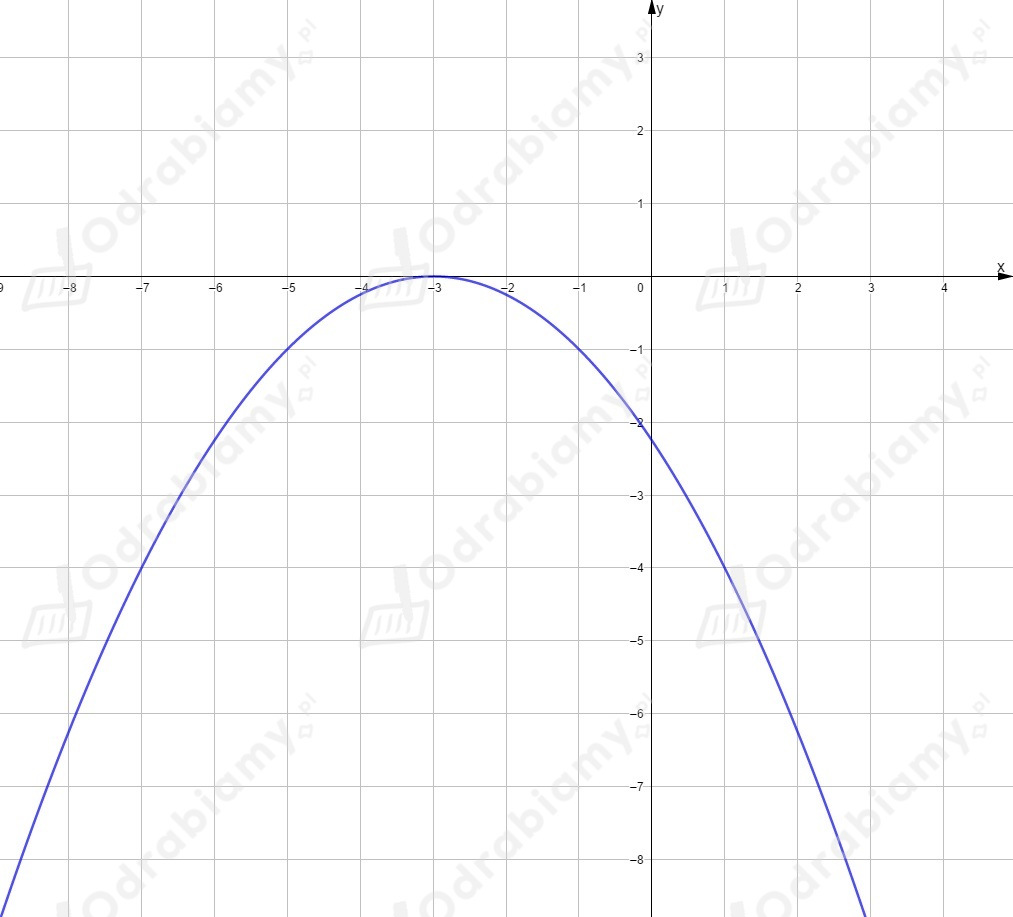
miejsca zerowe:

,

współrzędne wierzchołka:

 ,

współrzędne punktu przecięcia z osią 

.

Własności funkcji:

dziedziną jest zbiór , 

zbiorem wartości jest przedział ,  

funkcja przyjmuje wartość największą równą  dla  i nie przyjmuje wartości najmniejszej,

miejscem zerowym funkcji jest argument  ,

 dla  ,

osią symetrii wykresu jest prosta ,

funkcja jest rosnąca w przedziale   ,
funkcja jest malejąca w przedziale ,

równanie     
dla  ma dwa rozwiązania,
dla  ma jedno rozwiązanie,
dla  nie ma rozwiązań.