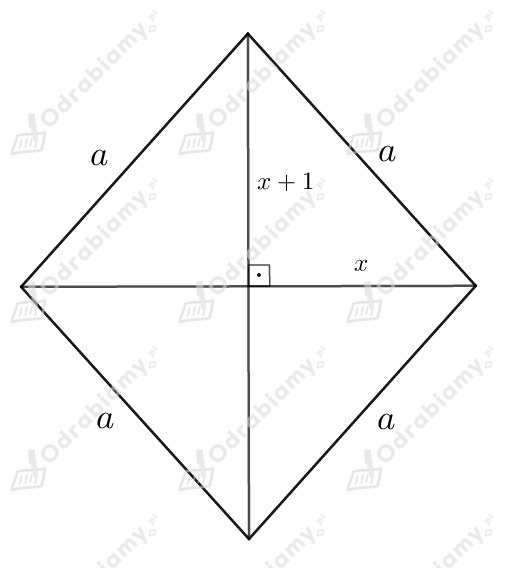
Boki rombu są równej długości, oznaczymy jest literką  .

Z treści zadania wiemy, że obwód tego rombu jest równy  , zatem  

Przekątne w rombie przecinają się pod kątem prostym i w połowie.

Długości przekątnych różnią się o  , więc możemy zapisać:

Długość pierwszej przekątnej: 

Długość połowy pierwszej przekątnej:   

Długość drugiej przekątnej: 

Długość połowy drugiej przekątnej:   

Zobaczmy jak wygląda to na rysunku

Mamy 4 trójkąty prostokątne. Wszystkie one są przystające (takie same).

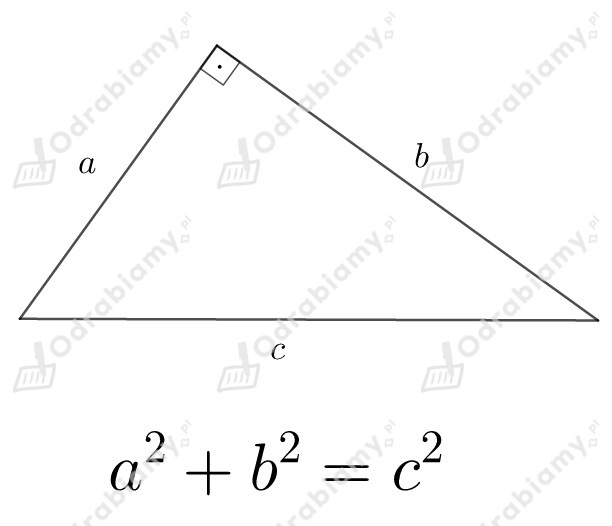
Aby obliczyć długości przekątnych, wystarczy skorzystać z twierdzenia Pitagorasa.

Jeśli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych

jest równa kwadratowi długości przeciwprostokątnej.

Zatem 

Rozwiązujemy powyższe równanie kwadratowe

 - nie może być rozwiązaniem,

ponieważ długość boku musi być liczbą dodatnią.

Długość połowy krótszej przekątnej wynosi  , zatem cała krótsza przekątna ma długość  .

Długość dłuższej przekątnej wynosi  .