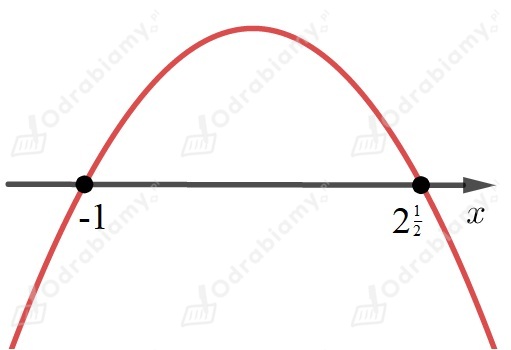
Obliczamy  i miejsca zerowe funkcji.

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Aby rozwiązać nierówność kwadratową, nie musimy dokładnie rysować paraboli.

Wystarczy zaznaczyć miejsca zerowe na osi   

i sprawdzić czy ramiona paraboli skierowane są do góry czy do dołu.

Wracamy do nierówności .

Odczytujemy z wykresu  , dla których nierówność jest spełniona

.

Przedział jest obustronnie otwarty, ponieważ szukamy takich ,

dla których  jest mniejsze od , a nie równe . 

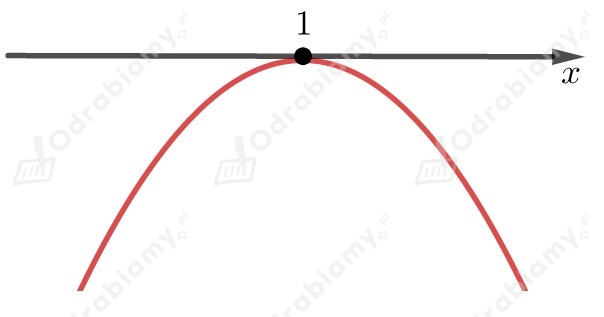
Współczynnik przy najwyższej potędze jest liczbą mniejszą od  

,

dlatego ramiona paraboli są skierowane do dołu.

Odczytujemy z wykresu  , dla których nierówność jest spełniona

.

Przedział jest obustronnie domknięty, ponieważ szukamy takich ,

dla których   jest większe lub równe .

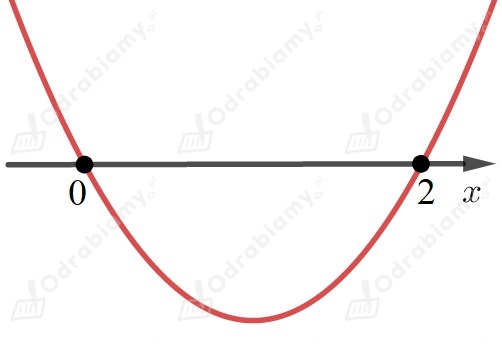
Zaczynamy od odjęcia od obu stron równania  

Sprawdzamy dla jakich  spełnione będzie równanie równanie .

 lub  .

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.

Przedział jest obustronnie otwarty, ponieważ szukamy takich , dla których

 jest większe od , a nie równe .

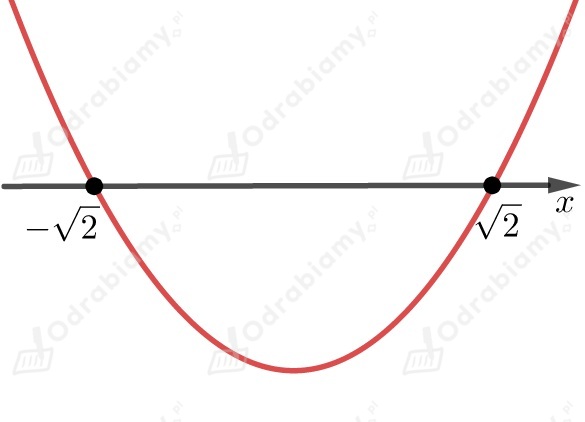
Zaczynamy od odjęcia od obu stron równania  

Korzystamy ze wzoru skróconego mnożenia  

Sprawdzamy dla jakich  spełnione będzie równanie równanie  .

 lub    

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność jest spełniona

.

Przedział jest obustronnie domknięty, ponieważ szukamy takich ,

dla których   jest większe lub równe .

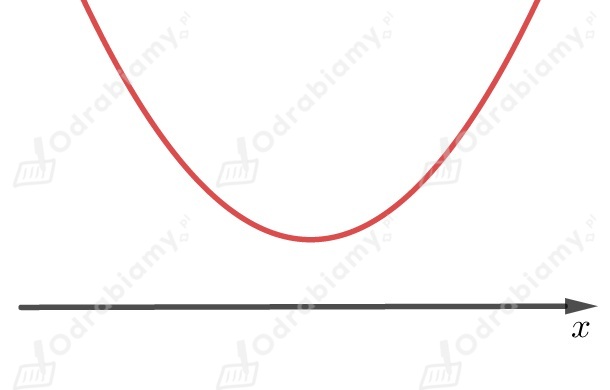
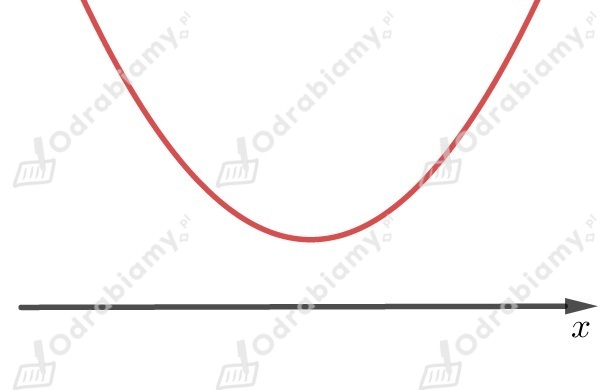
Równanie  nie rozwiązań (miejsc zerowych).

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.

Brak rozwiązań. 

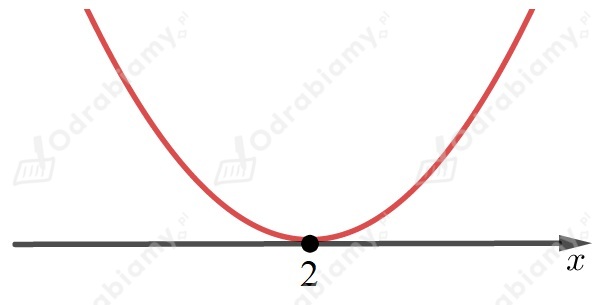
Współczynnik przy najwyższej potędze jest liczbą mniejszą od  

,

dlatego ramiona paraboli są skierowane do dołu.

Odczytujemy z wykresu  , dla których nierówność jest spełniona

.

Rozwiązaniem nierówności jest tylko jeden punkt.

Równanie  nie rozwiązań (miejsc zerowych).

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.

Brak rozwiązań. 

Zaczynamy od odjęcia od obu stron równania  

Możemy obliczać  i miejsce zerowe, ale zauważamy

wzór skróconego mnożenia  

Sprawdzamy dla jakich  spełnione będzie równanie równanie .

.  

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.

Brak rozwiązań.