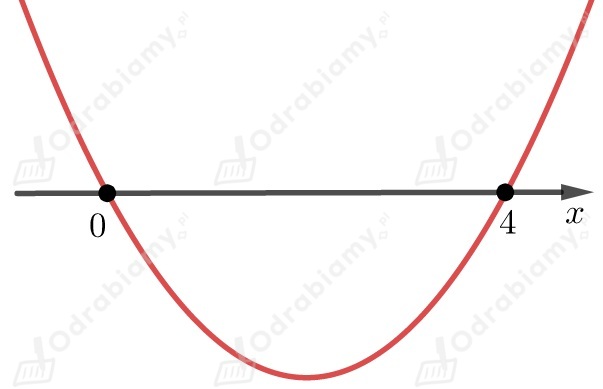
Obliczamy  i miejsca zerowe funkcji.

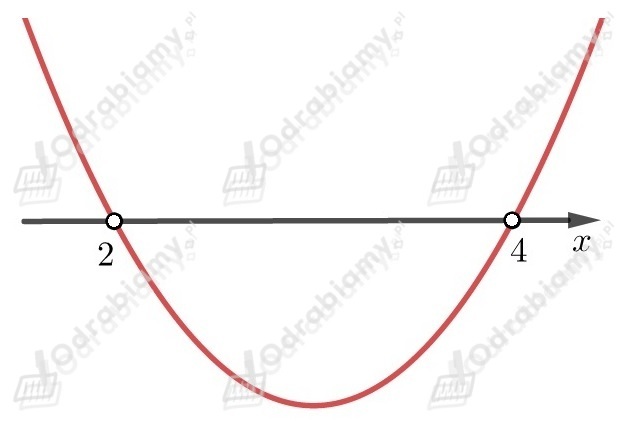
Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Wracamy do nierówności .

Odczytujemy z wykresu , dla których  nierówność jest spełniona

.

Przedział jest obustronnie otwarty ponieważ szukamy takich ,

dla których  jest większe od . 

Zaczynamy od odjęcia liczby  od obu stron równania  

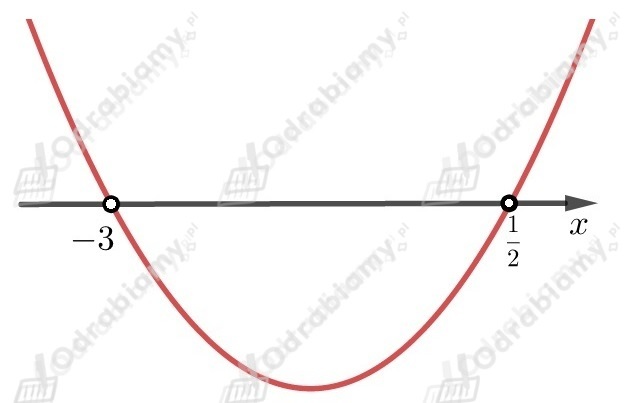
Współczynnik przy najwyższej potędze jest liczbą większą od  

,

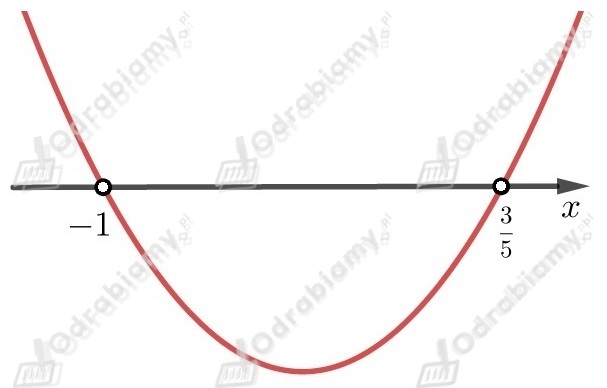
dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność jest spełniona

.

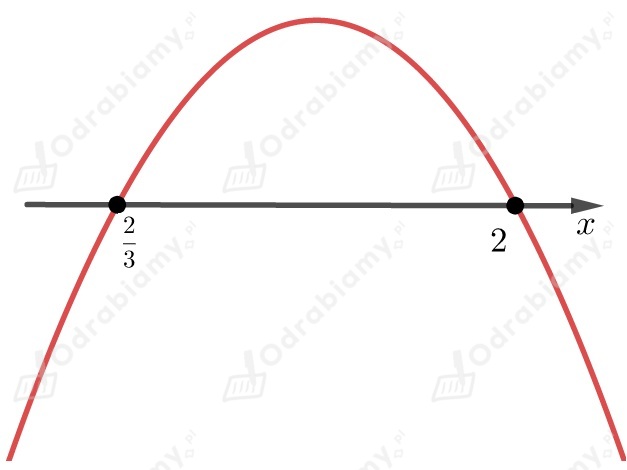
Współczynnik przy najwyższej potędze jest liczbą mniejszą od  

,

dlatego ramiona paraboli są skierowane do dołu.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.

Każda liczba poniesiona do kwadratu jest większa lub równa .

Po pomnożeniu takiej liczby przez  i dodaniu do niej jeszcze liczby   otrzymamy liczbę większą od .

Nierówność ta nie ma rozwiązania.

.

Możemy też postępować jak w powyższych przykładach.

Obliczając   otrzymamy liczbę ujemną, co oznacza brak jest miejsc zerowych.

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

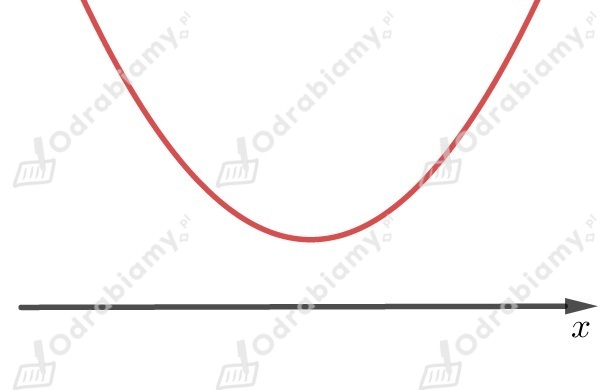
Wykres będzie wyglądał następująco: 

Widzimy, że nie ma takich , dla których wykres leży pod osią .

Zaczynamy od odjęcia   i   od obu stron równania 

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność jest spełniona

.

Równanie  nie rozwiązań (miejsc zerowych).

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność   jest spełniona

.

Rozwiązaniem nierówności jest cały zbiór liczb rzeczywistych.

Zaczynamy od przekształcenia równania,

korzystamy ze wzoru skróconego mnożenia  

Sprawdzamy, dla jakich   spełnione jest równanie      

 lub    

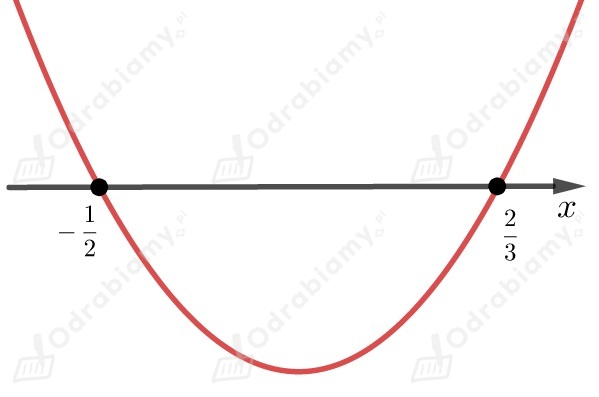
Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.

Współczynnik przy najwyższej potędze jest liczbą większą od  

,

dlatego ramiona paraboli są skierowane do góry.

Odczytujemy z wykresu  , dla których nierówność  jest spełniona

.