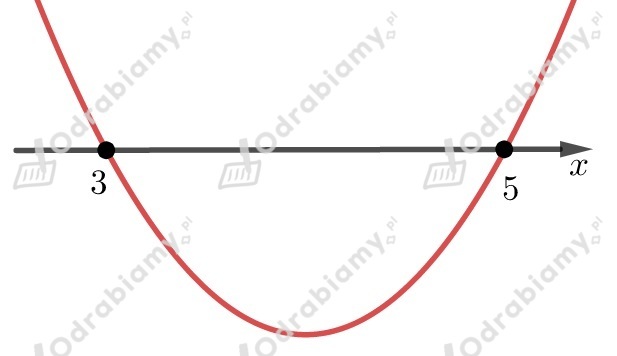
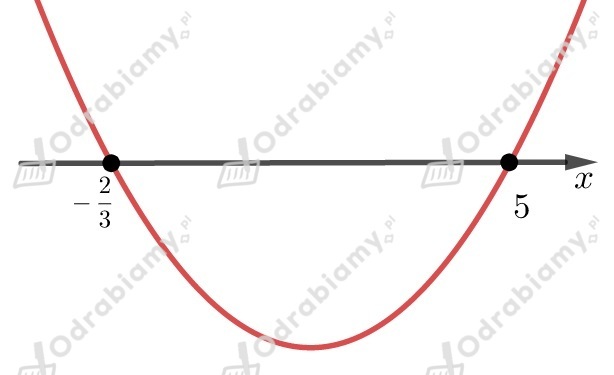
Liczby  i  będą miejscami zerowymi naszej funkcji,

którą możemy zapisać w postaci iloczynowej

Współczynnik przy najwyższej potędze jest liczbą większą od  

  (mnożymy współczynniki stojące przy ),

dlatego ramiona paraboli są skierowane do góry.

Przedział  jest rozwiązaniem nierówności  .

Mamy jednak podać przykład nierówności kwadratowej, w której znak nierówności zwrócony jest w drugą stronę.

UWAGA! Jeśli  , to  

np. 

 , więc    

Zatem skoro , to .

Zauważmy, że przedział  może być rozwiązaniem wszystkich nierówności postaci

, gdzie .

Powyższą nierówność zapiszmy jeszcze w żądanej postaci.

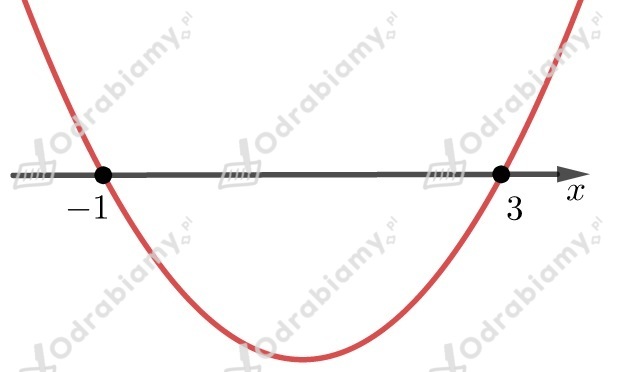
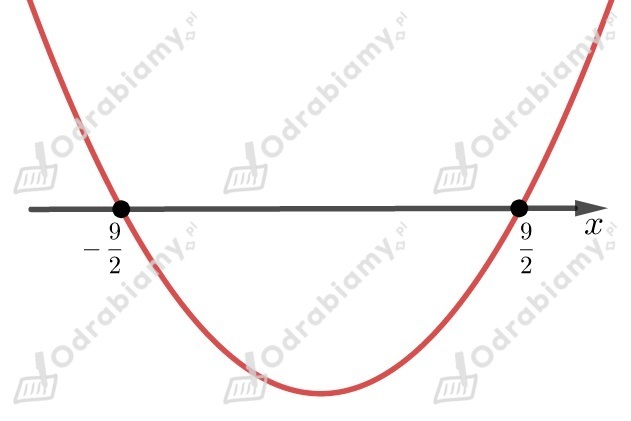
Liczby  i  będą miejscami zerowymi naszej funkcji,

którą możemy zapisać w postaci iloczynowej

Współczynnik przy najwyższej potędze jest liczbą większą od  

  (mnożymy współczynniki stojące przy  ),

dlatego ramiona paraboli są skierowane do góry.

Przedział  jest rozwiązaniem nierówności .

Zauważmy, że przedział  może być rozwiązaniem wszystkich nierówności postaci

, gdzie . 

Powyższą nierówność zapiszmy jeszcze w żądanej postaci.

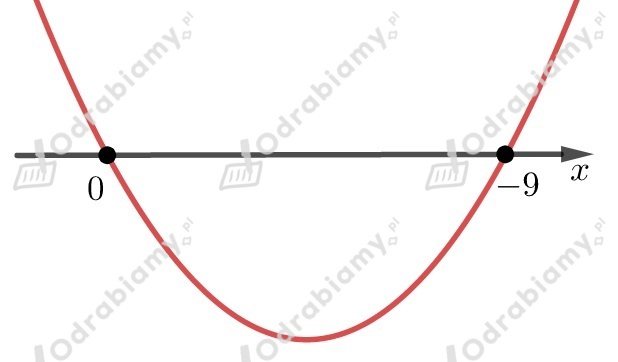
Liczby  i  będą miejscami zerowymi naszej funkcji,

którą możemy zapisać w postaci iloczynowej

Współczynnik przy najwyższej potędze jest liczbą większą od   

 (mnożymy współczynniki stojące przy ),

dlatego ramiona paraboli są skierowane do góry.

Przedział  jest rozwiązaniem nierówności .

Mamy jednak podać przykład nierówności kwadratowej, w której znak nierówności zwrócony jest w drugą stronę.

UWAGA! Jeśli  , to  

np. 

 , więc    

Zatem skoro , to .

Zauważmy, że przedział  może być rozwiązaniem wszystkich nierówności postaci

  , gdzie .

Powyższą nierówność zapiszmy jeszcze w żądanej postaci.

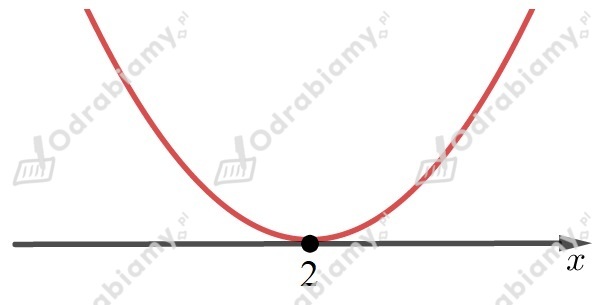
Liczba  miejscem zerowym naszej funkcji,

którą możemy zapisać w postaci iloczynowej

Współczynnik przy najwyższej potędze jest liczbą większą od   

 (mnożymy współczynniki stojące przy ),

dlatego ramiona paraboli są skierowane do góry.

Liczba   nie może być rozwiązaniem nierówności kwadratowej postaci .

Nie ma takiej nierówności.

Liczby  i  będą miejscami zerowymi naszej funkcji,

którą możemy zapisać w postaci iloczynowej

Współczynnik przy najwyższej potędze jest liczbą większą od    

 (mnożymy współczynniki stojące przy ),

dlatego ramiona paraboli są skierowane do góry.

Przedział  jest rozwiązaniem nierówności .

Zauważmy, że przedział  może być rozwiązaniem wszystkich nierówności postaci

, gdzie .

Powyższą nierówność zapiszmy jeszcze w żądanej postaci.

Liczby  i  będą miejscami zerowymi naszej funkcji,

którą możemy zapisać w postaci iloczynowej

Współczynnik przy najwyższej potędze jest liczbą większą od   

 (mnożymy współczynniki stojące przy ),

dlatego ramiona paraboli są skierowane do góry.

Przedział  jest rozwiązaniem nierówności .

Zauważmy, że przedział  może być rozwiązaniem wszystkich nierówności postaci

  , gdzie .

Powyższą nierówność zapiszmy jeszcze w żądanej postaci.